Turn on suggestions
Auto-suggest helps you quickly narrow down your search results by suggesting possible matches as you type.
Showing results for
Turn on suggestions
Auto-suggest helps you quickly narrow down your search results by suggesting possible matches as you type.
Showing results for
- Graphisoft Community (INT)
- :
- Forum
- :
- Libraries & objects
- :
- Some useful GDL scripts (in Italian)
Options
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Pin this post for me
- Bookmark
- Subscribe to Topic
- Mute
- Printer Friendly Page
Libraries & objects
About Archicad and BIMcloud libraries, their management and migration, objects and other library parts, etc.
Some useful GDL scripts (in Italian)
Anonymous
Not applicable
Options
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
2012-09-19 04:00 PM
2012-09-19
04:00 PM
This gentleman was nice enough to post some GDL scripts that may be useful for users of ArchiCAD. However, they are all in Italian.
What we decided is that we merge all these 7 posts into one thread.
YOu may try to use Google Translator to translate the text into English, then it will probably make more sense.
Le Corbusier.Modulor
La progressione geometrica
La serie in progressione geometrica è una successione di numeri dove il successivo si ottiene dal precedente moltiplicandolo per un fattore detto ragione della progressione.
La serie in progressione aritmetica è invece una successione di numeri dove il successivo si ottiene dal precedente aggiungendo un valore fisso.
Il primo tipo di serie è molto più importante per l’architettura, Le Corbusier lo utilizza nel Modulor utilizzando come ragione il numero aureo di Fibonacci = (sqr(5)+1)/2
Un esempio di successione geometrica:
m, m*ra, m*ra^2, … , m*ra^n, …
Ai fini del disegno con il calcolatore è importante poter calcolare la sommatoria di un numero arbitrario di elementi in successione geometrica.
(ra-1)*(1+ra+…+ra^n)= ra^(n+1)-1
1+ra+…+ra^n=(ra^(n+1)-1)/(ra-1)
m+m*ra2 … + m*ra^n=m*(ra^(n+1)-1)/(ra-1) !sommatoria di n+1 elementi
Ad esempio volendo costruire in 2D un reticolo in prospettiva frontale, mentre non ci sono problemi per costruire le ortogonali, senza la formula della sommatoria diventa impraticabile costruire le trasversali (a differenza del disegno fatto a mano, che sfrutta i punti di intersezione con una diagonale). Infatti le trasversali si dispongono in successione geometrica (vedi il mio testo:
Marco Masetti, La prospettiva scenica e tridimensionale, Pitagora editrice, Bologna,2009 a pag.46 ).
Nel testo 2D scrivere:
!inizio----------------------------------------
x=1
ra=.5 !ra<1 altrimenti le linee invece di infittirsi, si allontanano
m=.5
n=7 !fine parametri
for i=0 to n
line2 –x/2, m*(ra^(i+1)-1)/(ra-1), x/2, m*(ra^(i+1)-1)/(ra-1)
next i
line2 –x/2, m/ (1-ra), x/2, m/ (1-ra) !L.O., retta limite della successione
!fine----------------------------------------
Lo script costruisce n+2 rette orizzontali sovrapposte in successione geometrica.
Di fatto le rette si possono considerare come le trasversali di una prospettiva frontale con modulo oggettivo m e con linea di orizzonte a quota: m/ (1-ra)
Infatti con ra<1:
limite per n all’infinito: m*(ra^(n+1)-1)/(ra-1) = m*(- 1)/(ra-1)=m/ (1-ra)
Proviamo ora a “disegnare”, con l’algebra, il Modulor di Le Corbusier, che trovo a pag.298 del testo:
A.Marcolli, Teoria del campo, Firenze 1974
Il disegno lo costruiamo rovesciato, in modo da avere i valori decrescenti verso l’alto.
n=10 !numero iterazioni, fine parametri
fi=(sqr(5)+1)/2 !numero di Fibonacci, proporzione aurea: fi=1/(fi-1)
line2 0,0, 0,1 !asse verticale, la figura è alta 1, infatti: altezza totale 1-fi/2+1/(2*fi)/ (1-1/fi)=1
line2 -.2,1,.2,1 !asse limite
line2 -.2,0, .2,0 !linea base
line2 0,1-fi/2, .2,1-fi/2 !inizio segmenti destra, il primo a quota 1-fi/2
!i successivi segmenti orizzontali distanziati di 1/fi,1/fi^2, 1/fi^3,…
m=1/(2*fi) !ampiezza primo tratto a partire da quota 1-fi/2
ra=1/fi
for i=0 to n
line2 0,1-fi/2+m*(ra^(i+1)-1)/(ra-1), .2,1-fi/2+m*(ra^(i+1)-1)/(ra-1)
next I !è aggiunto 1-fi/2, perché è la quota di partenza della successione geometrica di ragione 1/fi
for i=0 to n-2
arc2 0,1-fi/2+m*(ra^(i+1)-1)/(ra-1), 1/2/fi^(i+1) ,-90, 90
next i
arc2 0,1-fi/2, 1-fi/2 ,90, 270 !inizio archi sinistra, sono centrati sui segmenti già definiti
for i=0 to n-1
arc2 0,1-fi/2+m*(ra^(i+1)-1)/(ra-1), (1-fi/2)*ra^(i+1) ,90, 270
next i
line2 0,2-fi, -.2,2-fi
for i=0 to n-1
line2 0,1-fi/2+m*(ra^(i+1)-1)/(ra-1)+(1-fi/2)*ra^(i+1),
-.2,1-fi/2+m*(ra^(i+1)-1)/(ra-1)+(1-fi/2)*ra^(i+1)
next i !segmenti definiti dal centro degli archi più il raggio

8 REPLIES 8
Anonymous
Not applicable
Options
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
2012-09-19 04:28 PM
2012-09-19
04:28 PM
!!!Istruzione per ottenere l'oggetto GDL dell'immagine.
!Elenco parametri -------------------------------------------:
n=6 !divisoni semimeridiano, integer
m=6 !divisoni lungo equatore, integer
t=0 !bit: =1 RGB, =0 CMYK
p=1 !pen
s="linee in vista" !abc
l="opaco" !abc
!Script parametri -------------------------------------------:
VALUES "t" "rgb","cmy"
VALUES "s" "linee in vista","colori"
VALUES "l" "opaco","metallo","plastica","vetro","brillante"
! TESTO 2D --------------------------------------------------:
if s="linee in vista" then w=2
if s="colori" then w=3
project2 3,270,w
!TESTO 3D ----------------------------------------------------:
pen p
if l="opaco" then w=2
if l="metallo" then w=3
if l="plastica" then w=4
if l="vetro" then w=5
if l="brillante" then w=6
!parte superiore lomgitudine 0-120 da green a blue, polo white
r1=not(t)*100
g1=t*100
b1=not(t)*100
r2=not(t)*100
g2=not(t)*100
b2=t*100
for j=0 to m-1
R3=(100-100/3)*sin(j*90/(m+2))+100/3
G3=(100-100/3)*sin(j*90/(m+2))+100/3
B3=(100-100/3)*sin(j*90/(m+2))+100/3
Re1=r1+j*(r3-r1)/m !i=0
Gr1=g1+j*(g3-g1)/m
Bu1=b1+j*(b3-b1)/m
Re2=r1+j*(r3-r1)/m+(r2+j*(r3-r2)/m-r1-j*(r3-r1)/m) !i=n-1
Gr2=g1+j*(g3-g1)/m+(g2+j*(g3-g2)/m-g1-j*(g3-g1)/m)
Bu2=b1+j*(b3-b1)/m+(b2+j*(b3-b2)/m-b1-j*(b3-b1)/m)
for k=0 to m-1-j
for i=0 to n-1 ! da re1,gr1,bu1 e re2,gr2,bu2 (arco 120°) a r3,g3,b3 (centro cerchio)
Re=re1+k*(r3-re1)/(m-j)+(re2+k*(r3-re2)/(m-j)-re1-k*(r3-re1)/(n))/(n)*i
Gr=gr1+k*(g3-gr1)/(m-j)+(gr2+k*(g3-gr2)/(m-j)-gr1-k*(g3-gr1)/(n))/(n)*i
Bu=bu1+k*(b3-bu1)/(m-j)+(bu2+k*(b3-bu2)/(m-j)-bu1-k*(b3-bu1)/(n))/(n)*i
DEFINE MATERIAL "aik" w,
Re/100,Gr/100,Bu/100
MATERIAL "aik"
base
vert cos(j*90/m)*cos(k*90/(m-j))*cos(i*120/n),cos(j*90/(m))*cos(k*90/(m-j))*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos(k*90/(m-j))*cos((i+1)*120/n),cos(j*90/(m))*cos(k*90/(m-j))*sin((i+1)*120/n),sin(j*90/m)!2
vert cos(j*90/m)*cos((k+1)*90/(m-j))*cos((i+1)*120/n),cos(j*90/(m))*cos((k+1)*90/(m-j))*sin((i+1)*120/n),sin(j*90/m)!3
vert cos(j*90/m)*cos((k+1)*90/(m-j))*cos(i*120/n),cos(j*90/(m))*cos((k+1)*90/(m-j))*sin(i*120/n),sin(j*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next k
next j
rotz 120
!parte superiore lomgitudine 120-240 da blue a red, polo white
r1=not(t)*100
g1=not(t)*100
b1=t*100
r2=t*100
g2=not(t)*100
b2=not(t)*100
for j=0 to m-1
R3=(100-100/3)*sin(j*90/(m+2))+100/3
G3=(100-100/3)*sin(j*90/(m+2))+100/3
B3=(100-100/3)*sin(j*90/(m+2))+100/3
Re1=r1+j*(r3-r1)/m !i=0
Gr1=g1+j*(g3-g1)/m
Bu1=b1+j*(b3-b1)/m
Re2=r1+j*(r3-r1)/m+(r2+j*(r3-r2)/m-r1-j*(r3-r1)/m) !i=n-1
Gr2=g1+j*(g3-g1)/m+(g2+j*(g3-g2)/m-g1-j*(g3-g1)/m)
Bu2=b1+j*(b3-b1)/m+(b2+j*(b3-b2)/m-b1-j*(b3-b1)/m)
for k=0 to m-1-j
for i=0 to n-1 ! da re1,gr1,bu1 e re2,gr2,bu2 (arco 120°) a r3,g3,b3 (centro cerchio)
Re=re1+k*(r3-re1)/(m-j)+(re2+k*(r3-re2)/(m-j)-re1-k*(r3-re1)/(n))/(n)*i
Gr=gr1+k*(g3-gr1)/(m-j)+(gr2+k*(g3-gr2)/(m-j)-gr1-k*(g3-gr1)/(n))/(n)*i
Bu=bu1+k*(b3-bu1)/(m-j)+(bu2+k*(b3-bu2)/(m-j)-bu1-k*(b3-bu1)/(n))/(n)*i
DEFINE MATERIAL "bik" w,
Re/100,Gr/100,Bu/100
MATERIAL "bik"
base
vert cos(j*90/m)*cos(k*90/(m-j))*cos(i*120/n),cos(j*90/(m))*cos(k*90/(m-j))*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos(k*90/(m-j))*cos((i+1)*120/n),cos(j*90/(m))*cos(k*90/(m-j))*sin((i+1)*120/n),sin(j*90/m)!2
vert cos(j*90/m)*cos((k+1)*90/(m-j))*cos((i+1)*120/n),cos(j*90/(m))*cos((k+1)*90/(m-j))*sin((i+1)*120/n),sin(j*90/m)!3
vert cos(j*90/m)*cos((k+1)*90/(m-j))*cos(i*120/n),cos(j*90/(m))*cos((k+1)*90/(m-j))*sin(i*120/n),sin(j*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next k
next j
rotz 120
!parte superiore lomgitudine 240-360 da red a green, polo white
r1=t*100
g1=not(t)*100
b1=not(t)*100
r2=not(t)*100
g2=t*100
b2=not(t)*100
for j=0 to m-1
R3=(100-100/3)*sin(j*90/(m+2))+100/3
G3=(100-100/3)*sin(j*90/(m+2))+100/3
B3=(100-100/3)*sin(j*90/(m+2))+100/3
Re1=r1+j*(r3-r1)/m !i=0
Gr1=g1+j*(g3-g1)/m
Bu1=b1+j*(b3-b1)/m
Re2=r1+j*(r3-r1)/m+(r2+j*(r3-r2)/m-r1-j*(r3-r1)/m) !i=n-1
Gr2=g1+j*(g3-g1)/m+(g2+j*(g3-g2)/m-g1-j*(g3-g1)/m)
Bu2=b1+j*(b3-b1)/m+(b2+j*(b3-b2)/m-b1-j*(b3-b1)/m)
for k=0 to m-1-j
for i=0 to n-1 ! da re1,gr1,bu1 e re2,gr2,bu2 (arco 120°) a r3,g3,b3 (centro cerchio)
Re=re1+k*(r3-re1)/(m-j)+(re2+k*(r3-re2)/(m-j)-re1-k*(r3-re1)/(n))/(n)*i
Gr=gr1+k*(g3-gr1)/(m-j)+(gr2+k*(g3-gr2)/(m-j)-gr1-k*(g3-gr1)/(n))/(n)*i
Bu=bu1+k*(b3-bu1)/(m-j)+(bu2+k*(b3-bu2)/(m-j)-bu1-k*(b3-bu1)/(n))/(n)*i
DEFINE MATERIAL "cik" w,
Re/100,Gr/100,Bu/100
MATERIAL "cik"
base
vert cos(j*90/m)*cos(k*90/(m-j))*cos(i*120/n),cos(j*90/(m))*cos(k*90/(m-j))*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos(k*90/(m-j))*cos((i+1)*120/n),cos(j*90/(m))*cos(k*90/(m-j))*sin((i+1)*120/n),sin(j*90/m)!2
vert cos(j*90/m)*cos((k+1)*90/(m-j))*cos((i+1)*120/n),cos(j*90/(m))*cos((k+1)*90/(m-j))*sin((i+1)*120/n),sin(j*90/m)!3
vert cos(j*90/m)*cos((k+1)*90/(m-j))*cos(i*120/n),cos(j*90/(m))*cos((k+1)*90/(m-j))*sin(i*120/n),sin(j*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next k
next j
rotz 120
mulz -1
!parte inferiore lomgitudine 0-120 da green a blue, polo black
r1=not(t)*100
g1=t*100
b1=not(t)*100
r2=not(t)*100
g2=not(t)*100
b2=t*100
for j=1 to m-1
R3=(-100/3)*sin(j*90/(m+2))+100/3
G3=(-100/3)*sin(j*90/(m+2))+100/3
B3=(-100/3)*sin(j*90/(m+2))+100/3
Re1=r1+j*(r3-r1)/m !i=0
Gr1=g1+j*(g3-g1)/m
Bu1=b1+j*(b3-b1)/m
Re2=r1+j*(r3-r1)/m+(r2+j*(r3-r2)/m-r1-j*(r3-r1)/m) !i=n-1
Gr2=g1+j*(g3-g1)/m+(g2+j*(g3-g2)/m-g1-j*(g3-g1)/m)
Bu2=b1+j*(b3-b1)/m+(b2+j*(b3-b2)/m-b1-j*(b3-b1)/m)
for k=0 to m-1-j
for i=0 to n-1 ! da re1,gr1,bu1 e re2,gr2,bu2 (arco 120°) a r3,g3,b3 (centro cerchio)
Re=re1+k*(r3-re1)/(m-j)+(re2+k*(r3-re2)/(m-j)-re1-k*(r3-re1)/(n))/(n)*i
Gr=gr1+k*(g3-gr1)/(m-j)+(gr2+k*(g3-gr2)/(m-j)-gr1-k*(g3-gr1)/(n))/(n)*i
Bu=bu1+k*(b3-bu1)/(m-j)+(bu2+k*(b3-bu2)/(m-j)-bu1-k*(b3-bu1)/(n))/(n)*i
DEFINE MATERIAL "ai" w,
Re/100,Gr/100,Bu/100
MATERIAL "ai"
base
vert cos(j*90/m)*cos(k*90/(m-j))*cos(i*120/n),cos(j*90/(m))*cos(k*90/(m-j))*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos(k*90/(m-j))*cos((i+1)*120/n),cos(j*90/(m))*cos(k*90/(m-j))*sin((i+1)*120/n),sin(j*90/m)!2
vert cos(j*90/m)*cos((k+1)*90/(m-j))*cos((i+1)*120/n),cos(j*90/(m))*cos((k+1)*90/(m-j))*sin((i+1)*120/n),sin(j*90/m)!3
vert cos(j*90/m)*cos((k+1)*90/(m-j))*cos(i*120/n),cos(j*90/(m))*cos((k+1)*90/(m-j))*sin(i*120/n),sin(j*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next k
next j
rotz 120
!parte inferiore lomgitudine 120-240 da blue a red, polo black
r1=not(t)*100
g1=not(t)*100
b1=t*100
r2=t*100
g2=not(t)*100
b2=not(t)*100
for j=1 to m-1
R3=(-100/3)*sin(j*90/(m+2))+100/3
G3=(-100/3)*sin(j*90/(m+2))+100/3
B3=(-100/3)*sin(j*90/(m+2))+100/3
Re1=r1+j*(r3-r1)/m !i=0
Gr1=g1+j*(g3-g1)/m
Bu1=b1+j*(b3-b1)/m
Re2=r1+j*(r3-r1)/m+(r2+j*(r3-r2)/m-r1-j*(r3-r1)/m) !i=n-1
Gr2=g1+j*(g3-g1)/m+(g2+j*(g3-g2)/m-g1-j*(g3-g1)/m)
Bu2=b1+j*(b3-b1)/m+(b2+j*(b3-b2)/m-b1-j*(b3-b1)/m)
for k=0 to m-1-j
for i=0 to n-1 ! da re1,gr1,bu1 e re2,gr2,bu2 (arco 120°) a r3,g3,b3 (centro cerchio)
Re=re1+k*(r3-re1)/(m-j)+(re2+k*(r3-re2)/(m-j)-re1-k*(r3-re1)/(n))/(n)*i
Gr=gr1+k*(g3-gr1)/(m-j)+(gr2+k*(g3-gr2)/(m-j)-gr1-k*(g3-gr1)/(n))/(n)*i
Bu=bu1+k*(b3-bu1)/(m-j)+(bu2+k*(b3-bu2)/(m-j)-bu1-k*(b3-bu1)/(n))/(n)*i
DEFINE MATERIAL "bi" w,
Re/100,Gr/100,Bu/100
MATERIAL "bi"
base
vert cos(j*90/m)*cos(k*90/(m-j))*cos(i*120/n),cos(j*90/(m))*cos(k*90/(m-j))*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos(k*90/(m-j))*cos((i+1)*120/n),cos(j*90/(m))*cos(k*90/(m-j))*sin((i+1)*120/n),sin(j*90/m)!2
vert cos(j*90/m)*cos((k+1)*90/(m-j))*cos((i+1)*120/n),cos(j*90/(m))*cos((k+1)*90/(m-j))*sin((i+1)*120/n),sin(j*90/m)!3
vert cos(j*90/m)*cos((k+1)*90/(m-j))*cos(i*120/n),cos(j*90/(m))*cos((k+1)*90/(m-j))*sin(i*120/n),sin(j*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next k
next j
rotz 120
!parte inferiore lomgitudine 240-360 da red a green, polo black
r1=t*100
g1=not(t)*100
b1=not(t)*100
r2=not(t)*100
g2=t*100
b2=not(t)*100
for j=1 to m-1
R3=(-100/3)*sin(j*90/(m+2))+100/3
G3=(-100/3)*sin(j*90/(m+2))+100/3
B3=(-100/3)*sin(j*90/(m+2))+100/3
Re1=r1+j*(r3-r1)/m !i=0
Gr1=g1+j*(g3-g1)/m
Bu1=b1+j*(b3-b1)/m
Re2=r1+j*(r3-r1)/m+(r2+j*(r3-r2)/m-r1-j*(r3-r1)/m) !i=n-1
Gr2=g1+j*(g3-g1)/m+(g2+j*(g3-g2)/m-g1-j*(g3-g1)/m)
Bu2=b1+j*(b3-b1)/m+(b2+j*(b3-b2)/m-b1-j*(b3-b1)/m)
for k=0 to m-1-j
for i=0 to n-1 ! da re1,gr1,bu1 e re2,gr2,bu2 (arco 120°) a r3,g3,b3 (centro cerchio)
Re=re1+k*(r3-re1)/(m-j)+(re2+k*(r3-re2)/(m-j)-re1-k*(r3-re1)/(n))/(n)*i
Gr=gr1+k*(g3-gr1)/(m-j)+(gr2+k*(g3-gr2)/(m-j)-gr1-k*(g3-gr1)/(n))/(n)*i
Bu=bu1+k*(b3-bu1)/(m-j)+(bu2+k*(b3-bu2)/(m-j)-bu1-k*(b3-bu1)/(n))/(n)*i
DEFINE MATERIAL "ci" w,
Re/100,Gr/100,Bu/100
MATERIAL "ci"
base
vert cos(j*90/m)*cos(k*90/(m-j))*cos(i*120/n),cos(j*90/(m))*cos(k*90/(m-j))*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos(k*90/(m-j))*cos((i+1)*120/n),cos(j*90/(m))*cos(k*90/(m-j))*sin((i+1)*120/n),sin(j*90/m)!2
vert cos(j*90/m)*cos((k+1)*90/(m-j))*cos((i+1)*120/n),cos(j*90/(m))*cos((k+1)*90/(m-j))*sin((i+1)*120/n),sin(j*90/m)!3
vert cos(j*90/m)*cos((k+1)*90/(m-j))*cos(i*120/n),cos(j*90/(m))*cos((k+1)*90/(m-j))*sin(i*120/n),sin(j*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next k
next j
del top
!Elenco parametri -------------------------------------------:
n=6 !divisoni semimeridiano, integer
m=6 !divisoni lungo equatore, integer
t=0 !bit: =1 RGB, =0 CMYK
p=1 !pen
s="linee in vista" !abc
l="opaco" !abc
!Script parametri -------------------------------------------:
VALUES "t" "rgb","cmy"
VALUES "s" "linee in vista","colori"
VALUES "l" "opaco","metallo","plastica","vetro","brillante"
! TESTO 2D --------------------------------------------------:
if s="linee in vista" then w=2
if s="colori" then w=3
project2 3,270,w
!TESTO 3D ----------------------------------------------------:
pen p
if l="opaco" then w=2
if l="metallo" then w=3
if l="plastica" then w=4
if l="vetro" then w=5
if l="brillante" then w=6
!parte superiore lomgitudine 0-120 da green a blue, polo white
r1=not(t)*100
g1=t*100
b1=not(t)*100
r2=not(t)*100
g2=not(t)*100
b2=t*100
for j=0 to m-1
R3=(100-100/3)*sin(j*90/(m+2))+100/3
G3=(100-100/3)*sin(j*90/(m+2))+100/3
B3=(100-100/3)*sin(j*90/(m+2))+100/3
Re1=r1+j*(r3-r1)/m !i=0
Gr1=g1+j*(g3-g1)/m
Bu1=b1+j*(b3-b1)/m
Re2=r1+j*(r3-r1)/m+(r2+j*(r3-r2)/m-r1-j*(r3-r1)/m) !i=n-1
Gr2=g1+j*(g3-g1)/m+(g2+j*(g3-g2)/m-g1-j*(g3-g1)/m)
Bu2=b1+j*(b3-b1)/m+(b2+j*(b3-b2)/m-b1-j*(b3-b1)/m)
for k=0 to m-1-j
for i=0 to n-1 ! da re1,gr1,bu1 e re2,gr2,bu2 (arco 120°) a r3,g3,b3 (centro cerchio)
Re=re1+k*(r3-re1)/(m-j)+(re2+k*(r3-re2)/(m-j)-re1-k*(r3-re1)/(n))/(n)*i
Gr=gr1+k*(g3-gr1)/(m-j)+(gr2+k*(g3-gr2)/(m-j)-gr1-k*(g3-gr1)/(n))/(n)*i
Bu=bu1+k*(b3-bu1)/(m-j)+(bu2+k*(b3-bu2)/(m-j)-bu1-k*(b3-bu1)/(n))/(n)*i
DEFINE MATERIAL "aik" w,
Re/100,Gr/100,Bu/100
MATERIAL "aik"
base
vert cos(j*90/m)*cos(k*90/(m-j))*cos(i*120/n),cos(j*90/(m))*cos(k*90/(m-j))*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos(k*90/(m-j))*cos((i+1)*120/n),cos(j*90/(m))*cos(k*90/(m-j))*sin((i+1)*120/n),sin(j*90/m)!2
vert cos(j*90/m)*cos((k+1)*90/(m-j))*cos((i+1)*120/n),cos(j*90/(m))*cos((k+1)*90/(m-j))*sin((i+1)*120/n),sin(j*90/m)!3
vert cos(j*90/m)*cos((k+1)*90/(m-j))*cos(i*120/n),cos(j*90/(m))*cos((k+1)*90/(m-j))*sin(i*120/n),sin(j*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next k
next j
rotz 120
!parte superiore lomgitudine 120-240 da blue a red, polo white
r1=not(t)*100
g1=not(t)*100
b1=t*100
r2=t*100
g2=not(t)*100
b2=not(t)*100
for j=0 to m-1
R3=(100-100/3)*sin(j*90/(m+2))+100/3
G3=(100-100/3)*sin(j*90/(m+2))+100/3
B3=(100-100/3)*sin(j*90/(m+2))+100/3
Re1=r1+j*(r3-r1)/m !i=0
Gr1=g1+j*(g3-g1)/m
Bu1=b1+j*(b3-b1)/m
Re2=r1+j*(r3-r1)/m+(r2+j*(r3-r2)/m-r1-j*(r3-r1)/m) !i=n-1
Gr2=g1+j*(g3-g1)/m+(g2+j*(g3-g2)/m-g1-j*(g3-g1)/m)
Bu2=b1+j*(b3-b1)/m+(b2+j*(b3-b2)/m-b1-j*(b3-b1)/m)
for k=0 to m-1-j
for i=0 to n-1 ! da re1,gr1,bu1 e re2,gr2,bu2 (arco 120°) a r3,g3,b3 (centro cerchio)
Re=re1+k*(r3-re1)/(m-j)+(re2+k*(r3-re2)/(m-j)-re1-k*(r3-re1)/(n))/(n)*i
Gr=gr1+k*(g3-gr1)/(m-j)+(gr2+k*(g3-gr2)/(m-j)-gr1-k*(g3-gr1)/(n))/(n)*i
Bu=bu1+k*(b3-bu1)/(m-j)+(bu2+k*(b3-bu2)/(m-j)-bu1-k*(b3-bu1)/(n))/(n)*i
DEFINE MATERIAL "bik" w,
Re/100,Gr/100,Bu/100
MATERIAL "bik"
base
vert cos(j*90/m)*cos(k*90/(m-j))*cos(i*120/n),cos(j*90/(m))*cos(k*90/(m-j))*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos(k*90/(m-j))*cos((i+1)*120/n),cos(j*90/(m))*cos(k*90/(m-j))*sin((i+1)*120/n),sin(j*90/m)!2
vert cos(j*90/m)*cos((k+1)*90/(m-j))*cos((i+1)*120/n),cos(j*90/(m))*cos((k+1)*90/(m-j))*sin((i+1)*120/n),sin(j*90/m)!3
vert cos(j*90/m)*cos((k+1)*90/(m-j))*cos(i*120/n),cos(j*90/(m))*cos((k+1)*90/(m-j))*sin(i*120/n),sin(j*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next k
next j
rotz 120
!parte superiore lomgitudine 240-360 da red a green, polo white
r1=t*100
g1=not(t)*100
b1=not(t)*100
r2=not(t)*100
g2=t*100
b2=not(t)*100
for j=0 to m-1
R3=(100-100/3)*sin(j*90/(m+2))+100/3
G3=(100-100/3)*sin(j*90/(m+2))+100/3
B3=(100-100/3)*sin(j*90/(m+2))+100/3
Re1=r1+j*(r3-r1)/m !i=0
Gr1=g1+j*(g3-g1)/m
Bu1=b1+j*(b3-b1)/m
Re2=r1+j*(r3-r1)/m+(r2+j*(r3-r2)/m-r1-j*(r3-r1)/m) !i=n-1
Gr2=g1+j*(g3-g1)/m+(g2+j*(g3-g2)/m-g1-j*(g3-g1)/m)
Bu2=b1+j*(b3-b1)/m+(b2+j*(b3-b2)/m-b1-j*(b3-b1)/m)
for k=0 to m-1-j
for i=0 to n-1 ! da re1,gr1,bu1 e re2,gr2,bu2 (arco 120°) a r3,g3,b3 (centro cerchio)
Re=re1+k*(r3-re1)/(m-j)+(re2+k*(r3-re2)/(m-j)-re1-k*(r3-re1)/(n))/(n)*i
Gr=gr1+k*(g3-gr1)/(m-j)+(gr2+k*(g3-gr2)/(m-j)-gr1-k*(g3-gr1)/(n))/(n)*i
Bu=bu1+k*(b3-bu1)/(m-j)+(bu2+k*(b3-bu2)/(m-j)-bu1-k*(b3-bu1)/(n))/(n)*i
DEFINE MATERIAL "cik" w,
Re/100,Gr/100,Bu/100
MATERIAL "cik"
base
vert cos(j*90/m)*cos(k*90/(m-j))*cos(i*120/n),cos(j*90/(m))*cos(k*90/(m-j))*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos(k*90/(m-j))*cos((i+1)*120/n),cos(j*90/(m))*cos(k*90/(m-j))*sin((i+1)*120/n),sin(j*90/m)!2
vert cos(j*90/m)*cos((k+1)*90/(m-j))*cos((i+1)*120/n),cos(j*90/(m))*cos((k+1)*90/(m-j))*sin((i+1)*120/n),sin(j*90/m)!3
vert cos(j*90/m)*cos((k+1)*90/(m-j))*cos(i*120/n),cos(j*90/(m))*cos((k+1)*90/(m-j))*sin(i*120/n),sin(j*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next k
next j
rotz 120
mulz -1
!parte inferiore lomgitudine 0-120 da green a blue, polo black
r1=not(t)*100
g1=t*100
b1=not(t)*100
r2=not(t)*100
g2=not(t)*100
b2=t*100
for j=1 to m-1
R3=(-100/3)*sin(j*90/(m+2))+100/3
G3=(-100/3)*sin(j*90/(m+2))+100/3
B3=(-100/3)*sin(j*90/(m+2))+100/3
Re1=r1+j*(r3-r1)/m !i=0
Gr1=g1+j*(g3-g1)/m
Bu1=b1+j*(b3-b1)/m
Re2=r1+j*(r3-r1)/m+(r2+j*(r3-r2)/m-r1-j*(r3-r1)/m) !i=n-1
Gr2=g1+j*(g3-g1)/m+(g2+j*(g3-g2)/m-g1-j*(g3-g1)/m)
Bu2=b1+j*(b3-b1)/m+(b2+j*(b3-b2)/m-b1-j*(b3-b1)/m)
for k=0 to m-1-j
for i=0 to n-1 ! da re1,gr1,bu1 e re2,gr2,bu2 (arco 120°) a r3,g3,b3 (centro cerchio)
Re=re1+k*(r3-re1)/(m-j)+(re2+k*(r3-re2)/(m-j)-re1-k*(r3-re1)/(n))/(n)*i
Gr=gr1+k*(g3-gr1)/(m-j)+(gr2+k*(g3-gr2)/(m-j)-gr1-k*(g3-gr1)/(n))/(n)*i
Bu=bu1+k*(b3-bu1)/(m-j)+(bu2+k*(b3-bu2)/(m-j)-bu1-k*(b3-bu1)/(n))/(n)*i
DEFINE MATERIAL "ai" w,
Re/100,Gr/100,Bu/100
MATERIAL "ai"
base
vert cos(j*90/m)*cos(k*90/(m-j))*cos(i*120/n),cos(j*90/(m))*cos(k*90/(m-j))*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos(k*90/(m-j))*cos((i+1)*120/n),cos(j*90/(m))*cos(k*90/(m-j))*sin((i+1)*120/n),sin(j*90/m)!2
vert cos(j*90/m)*cos((k+1)*90/(m-j))*cos((i+1)*120/n),cos(j*90/(m))*cos((k+1)*90/(m-j))*sin((i+1)*120/n),sin(j*90/m)!3
vert cos(j*90/m)*cos((k+1)*90/(m-j))*cos(i*120/n),cos(j*90/(m))*cos((k+1)*90/(m-j))*sin(i*120/n),sin(j*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next k
next j
rotz 120
!parte inferiore lomgitudine 120-240 da blue a red, polo black
r1=not(t)*100
g1=not(t)*100
b1=t*100
r2=t*100
g2=not(t)*100
b2=not(t)*100
for j=1 to m-1
R3=(-100/3)*sin(j*90/(m+2))+100/3
G3=(-100/3)*sin(j*90/(m+2))+100/3
B3=(-100/3)*sin(j*90/(m+2))+100/3
Re1=r1+j*(r3-r1)/m !i=0
Gr1=g1+j*(g3-g1)/m
Bu1=b1+j*(b3-b1)/m
Re2=r1+j*(r3-r1)/m+(r2+j*(r3-r2)/m-r1-j*(r3-r1)/m) !i=n-1
Gr2=g1+j*(g3-g1)/m+(g2+j*(g3-g2)/m-g1-j*(g3-g1)/m)
Bu2=b1+j*(b3-b1)/m+(b2+j*(b3-b2)/m-b1-j*(b3-b1)/m)
for k=0 to m-1-j
for i=0 to n-1 ! da re1,gr1,bu1 e re2,gr2,bu2 (arco 120°) a r3,g3,b3 (centro cerchio)
Re=re1+k*(r3-re1)/(m-j)+(re2+k*(r3-re2)/(m-j)-re1-k*(r3-re1)/(n))/(n)*i
Gr=gr1+k*(g3-gr1)/(m-j)+(gr2+k*(g3-gr2)/(m-j)-gr1-k*(g3-gr1)/(n))/(n)*i
Bu=bu1+k*(b3-bu1)/(m-j)+(bu2+k*(b3-bu2)/(m-j)-bu1-k*(b3-bu1)/(n))/(n)*i
DEFINE MATERIAL "bi" w,
Re/100,Gr/100,Bu/100
MATERIAL "bi"
base
vert cos(j*90/m)*cos(k*90/(m-j))*cos(i*120/n),cos(j*90/(m))*cos(k*90/(m-j))*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos(k*90/(m-j))*cos((i+1)*120/n),cos(j*90/(m))*cos(k*90/(m-j))*sin((i+1)*120/n),sin(j*90/m)!2
vert cos(j*90/m)*cos((k+1)*90/(m-j))*cos((i+1)*120/n),cos(j*90/(m))*cos((k+1)*90/(m-j))*sin((i+1)*120/n),sin(j*90/m)!3
vert cos(j*90/m)*cos((k+1)*90/(m-j))*cos(i*120/n),cos(j*90/(m))*cos((k+1)*90/(m-j))*sin(i*120/n),sin(j*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next k
next j
rotz 120
!parte inferiore lomgitudine 240-360 da red a green, polo black
r1=t*100
g1=not(t)*100
b1=not(t)*100
r2=not(t)*100
g2=t*100
b2=not(t)*100
for j=1 to m-1
R3=(-100/3)*sin(j*90/(m+2))+100/3
G3=(-100/3)*sin(j*90/(m+2))+100/3
B3=(-100/3)*sin(j*90/(m+2))+100/3
Re1=r1+j*(r3-r1)/m !i=0
Gr1=g1+j*(g3-g1)/m
Bu1=b1+j*(b3-b1)/m
Re2=r1+j*(r3-r1)/m+(r2+j*(r3-r2)/m-r1-j*(r3-r1)/m) !i=n-1
Gr2=g1+j*(g3-g1)/m+(g2+j*(g3-g2)/m-g1-j*(g3-g1)/m)
Bu2=b1+j*(b3-b1)/m+(b2+j*(b3-b2)/m-b1-j*(b3-b1)/m)
for k=0 to m-1-j
for i=0 to n-1 ! da re1,gr1,bu1 e re2,gr2,bu2 (arco 120°) a r3,g3,b3 (centro cerchio)
Re=re1+k*(r3-re1)/(m-j)+(re2+k*(r3-re2)/(m-j)-re1-k*(r3-re1)/(n))/(n)*i
Gr=gr1+k*(g3-gr1)/(m-j)+(gr2+k*(g3-gr2)/(m-j)-gr1-k*(g3-gr1)/(n))/(n)*i
Bu=bu1+k*(b3-bu1)/(m-j)+(bu2+k*(b3-bu2)/(m-j)-bu1-k*(b3-bu1)/(n))/(n)*i
DEFINE MATERIAL "ci" w,
Re/100,Gr/100,Bu/100
MATERIAL "ci"
base
vert cos(j*90/m)*cos(k*90/(m-j))*cos(i*120/n),cos(j*90/(m))*cos(k*90/(m-j))*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos(k*90/(m-j))*cos((i+1)*120/n),cos(j*90/(m))*cos(k*90/(m-j))*sin((i+1)*120/n),sin(j*90/m)!2
vert cos(j*90/m)*cos((k+1)*90/(m-j))*cos((i+1)*120/n),cos(j*90/(m))*cos((k+1)*90/(m-j))*sin((i+1)*120/n),sin(j*90/m)!3
vert cos(j*90/m)*cos((k+1)*90/(m-j))*cos(i*120/n),cos(j*90/(m))*cos((k+1)*90/(m-j))*sin(i*120/n),sin(j*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next k
next j
del top
Anonymous
Not applicable
Options
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
2012-09-19 04:40 PM
2012-09-19
04:40 PM
Il colore che sul contorno è secondario, passando lungo il diametro,
si trasforma dalla parte opposta nel suo complementare.
Dato che l centro si è posto il grigio medio,
in teoria il cerchio dovrebbe rappresentare ogni tonalità,
essendo la sezione equatoriale della sfera dei colori.
Un colore, che ad esempio cada in un cerchio interno, per cambiare la sola tonalità,
dovrebbe ruotare attorno al centro, mantenendo invariato il raggio.
Spostandosi invece lungo il raggio cambia la saturazione dello stesso colore.
La luminosità è qui esclusa, perchè occorre salire o scendere verso i poli.
Inserendo valori m e n diversi si creano colori discontinui
perchè si esce dall' intervallo 0-1.
!!!Istruzioni per ottenere l'oggetto GDL in figura
!Elenco parametri -------------------------------------------:
n=12 !divisoni semimeridiano
m=12 !divisoni lungo equatore
t=0 !bit: =1 RGB, =0 CMYK
p=1 !pen
s="linee in vista" !abc
l="opaco" !abc
x=50 !saturazione 0-100
o=1 !bit mostra in 2D
!Script parametri -------------------------------------------:
VALUES "s" "linee in vista","colori"
VALUES "l" "opaco","metallo","plastica","vetro","brillante"
! TESTO 2D --------------------------------------------------:
if s="linee in vista" then w=2
if s="colori" then w=3
if o=1 then project2 3,270,w
mul2 a,b
if o=0 then circle2 0,0,1
!TESTO 3D ----------------------------------------------------:
pen p
mulx a
muly b
if l="opaco" then w=2
if l="metallo" then w=3
if l="plastica" then w=4
if l="vetro" then w=5
if l="brillante" then w=6
!0-120 da green a blue, centro grigio medio
r1=not(t)*100
g1=t*100
b1=not(t)*100
r2=not(t)*100
g2=not(t)*100
b2=t*100
r3=100/3
g3=100/3
b3=100/3
for j=0 to m-1
for i=0 to n-1 ! da r1,g1,b1 e r2,g2,b2 (arco 120°) a r3,g3,b3 (centro cerchio)
Re=r1+j*(r3-r1)/(n-1)+(r2+j*(r3-r2)/(n-1)-r1-j*(r3-r1)/(n-1))/(m-1)*i
Gr=g1+j*(g3-g1)/(n-1)+(g2+j*(g3-g2)/(n-1)-g1-j*(g3-g1)/(n-1))/(m-1)*i
Bu=b1+j*(b3-b1)/(n-1)+(b2+j*(b3-b2)/(n-1)-b1-j*(b3-b1)/(n-1))/(m-1)*i
DEFINE MATERIAL "aij" w,
Re/100,Gr/100,Bu/100
MATERIAL "aij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),0!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),0!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),0!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),0!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
!120-240 da blue a red, centro grigio medio
r1=not(t)*100
g1=not(t)*100
b1=t*100
r2=t*100
g2=not(t)*100
b2=not(t)*100
r3=100/3
g3=100/3
b3=100/3
for j=0 to m-1
for i=0 to n-1 ! da r1,g1,b1 e r2,g2,b2 (arco 120°) a r3,g3,b3 (centro cerchio)
Re=r1+j*(r3-r1)/(n-1)+(r2+j*(r3-r2)/(n-1)-r1-j*(r3-r1)/(n-1))/(m-1)*i
Gr=g1+j*(g3-g1)/(n-1)+(g2+j*(g3-g2)/(n-1)-g1-j*(g3-g1)/(n-1))/(m-1)*i
Bu=b1+j*(b3-b1)/(n-1)+(b2+j*(b3-b2)/(n-1)-b1-j*(b3-b1)/(n-1))/(m-1)*i
DEFINE MATERIAL "bij" w,
Re/100,Gr/100,Bu/100
MATERIAL "bij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),0!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),0!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),0!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),0!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
!240-360 da red a green, centro grigio medio
r1=t*100
g1=not(t)*100
b1=not(t)*100
r2=not(t)*100
g2=t*100
b2=not(t)*100
r3=100/3
g3=100/3
b3=100/3
for j=0 to m-1
for i=0 to n-1 ! da r1,g1,b1 e r2,g2,b2 (arco 120°) a r3,g3,b3 (centro cerchio)
Re=r1+j*(r3-r1)/(n-1)+(r2+j*(r3-r2)/(n-1)-r1-j*(r3-r1)/(n-1))/(m-1)*i
Gr=g1+j*(g3-g1)/(n-1)+(g2+j*(g3-g2)/(n-1)-g1-j*(g3-g1)/(n-1))/(m-1)*i
Bu=b1+j*(b3-b1)/(n-1)+(b2+j*(b3-b2)/(n-1)-b1-j*(b3-b1)/(n-1))/(m-1)*i
DEFINE MATERIAL "cij" w,
Re/100,Gr/100,Bu/100
MATERIAL "cij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),0!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),0!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),0!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),0!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
del top
si trasforma dalla parte opposta nel suo complementare.
Dato che l centro si è posto il grigio medio,
in teoria il cerchio dovrebbe rappresentare ogni tonalità,
essendo la sezione equatoriale della sfera dei colori.
Un colore, che ad esempio cada in un cerchio interno, per cambiare la sola tonalità,
dovrebbe ruotare attorno al centro, mantenendo invariato il raggio.
Spostandosi invece lungo il raggio cambia la saturazione dello stesso colore.
La luminosità è qui esclusa, perchè occorre salire o scendere verso i poli.
Inserendo valori m e n diversi si creano colori discontinui
perchè si esce dall' intervallo 0-1.
!!!Istruzioni per ottenere l'oggetto GDL in figura
!Elenco parametri -------------------------------------------:
n=12 !divisoni semimeridiano
m=12 !divisoni lungo equatore
t=0 !bit: =1 RGB, =0 CMYK
p=1 !pen
s="linee in vista" !abc
l="opaco" !abc
x=50 !saturazione 0-100
o=1 !bit mostra in 2D
!Script parametri -------------------------------------------:
VALUES "s" "linee in vista","colori"
VALUES "l" "opaco","metallo","plastica","vetro","brillante"
! TESTO 2D --------------------------------------------------:
if s="linee in vista" then w=2
if s="colori" then w=3
if o=1 then project2 3,270,w
mul2 a,b
if o=0 then circle2 0,0,1
!TESTO 3D ----------------------------------------------------:
pen p
mulx a
muly b
if l="opaco" then w=2
if l="metallo" then w=3
if l="plastica" then w=4
if l="vetro" then w=5
if l="brillante" then w=6
!0-120 da green a blue, centro grigio medio
r1=not(t)*100
g1=t*100
b1=not(t)*100
r2=not(t)*100
g2=not(t)*100
b2=t*100
r3=100/3
g3=100/3
b3=100/3
for j=0 to m-1
for i=0 to n-1 ! da r1,g1,b1 e r2,g2,b2 (arco 120°) a r3,g3,b3 (centro cerchio)
Re=r1+j*(r3-r1)/(n-1)+(r2+j*(r3-r2)/(n-1)-r1-j*(r3-r1)/(n-1))/(m-1)*i
Gr=g1+j*(g3-g1)/(n-1)+(g2+j*(g3-g2)/(n-1)-g1-j*(g3-g1)/(n-1))/(m-1)*i
Bu=b1+j*(b3-b1)/(n-1)+(b2+j*(b3-b2)/(n-1)-b1-j*(b3-b1)/(n-1))/(m-1)*i
DEFINE MATERIAL "aij" w,
Re/100,Gr/100,Bu/100
MATERIAL "aij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),0!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),0!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),0!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),0!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
!120-240 da blue a red, centro grigio medio
r1=not(t)*100
g1=not(t)*100
b1=t*100
r2=t*100
g2=not(t)*100
b2=not(t)*100
r3=100/3
g3=100/3
b3=100/3
for j=0 to m-1
for i=0 to n-1 ! da r1,g1,b1 e r2,g2,b2 (arco 120°) a r3,g3,b3 (centro cerchio)
Re=r1+j*(r3-r1)/(n-1)+(r2+j*(r3-r2)/(n-1)-r1-j*(r3-r1)/(n-1))/(m-1)*i
Gr=g1+j*(g3-g1)/(n-1)+(g2+j*(g3-g2)/(n-1)-g1-j*(g3-g1)/(n-1))/(m-1)*i
Bu=b1+j*(b3-b1)/(n-1)+(b2+j*(b3-b2)/(n-1)-b1-j*(b3-b1)/(n-1))/(m-1)*i
DEFINE MATERIAL "bij" w,
Re/100,Gr/100,Bu/100
MATERIAL "bij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),0!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),0!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),0!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),0!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
!240-360 da red a green, centro grigio medio
r1=t*100
g1=not(t)*100
b1=not(t)*100
r2=not(t)*100
g2=t*100
b2=not(t)*100
r3=100/3
g3=100/3
b3=100/3
for j=0 to m-1
for i=0 to n-1 ! da r1,g1,b1 e r2,g2,b2 (arco 120°) a r3,g3,b3 (centro cerchio)
Re=r1+j*(r3-r1)/(n-1)+(r2+j*(r3-r2)/(n-1)-r1-j*(r3-r1)/(n-1))/(m-1)*i
Gr=g1+j*(g3-g1)/(n-1)+(g2+j*(g3-g2)/(n-1)-g1-j*(g3-g1)/(n-1))/(m-1)*i
Bu=b1+j*(b3-b1)/(n-1)+(b2+j*(b3-b2)/(n-1)-b1-j*(b3-b1)/(n-1))/(m-1)*i
DEFINE MATERIAL "cij" w,
Re/100,Gr/100,Bu/100
MATERIAL "cij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),0!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),0!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),0!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),0!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
del top
Anonymous
Not applicable
Options
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
2012-09-19 04:54 PM
2012-09-19
04:54 PM
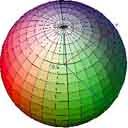
Sfera a tre colori
Per inserire i valori rgb ai 4 angoli del rettangolo è stata utilizzata la superficie:
z=(z1+(z3-z1)/dy*y)+(z2+(z4-z2)/dy*y-z1-(z3-z1)/dy)/dx*x
che definisce un iperboloide rigato a sella sopra il rettangolo di lati dx e dy che tocca O,
passante per i punti 1:0,0,z1 2:dx,0,z2 4:dx,dy,z4 3:0,dy,z3.
Poichè i valori oscillano entro i limiti, non si creano discontinuità tra i colori.
!!!Istruzioni per ottenere l'oggetto GDL in figura
!Elenco parametri -------------------------------------------:
n=12 !divisoni semimeridiano
m=12 !divisoni lungo equatore
t=0 !bit: =1 RGB, =0 CMYK
p=1 !pen
s="linee in vista" !abc
l="opaco" !abc
!Script parametri -------------------------------------------:
VALUES "s" "linee in vista","colori"
VALUES "l" "opaco","metallo","plastica","vetro","brillante"
! TESTO 2D --------------------------------------------------:
if s="linee in vista" then w=2
if s="colori" then w=3
project2 3,270,w
!TESTO 3D ----------------------------------------------------:
pen p
if l="opaco" then w=2
if l="metallo" then w=3
if l="plastica" then w=4
if l="vetro" then w=5
if l="brillante" then w=6
!parte superiore lomgitudine 0-120 da green a blue, polo white
r1=not(t)*100
g1=t*100
b1=not(t)*100
r2=not(t)*100
g2=not(t)*100
b2=t*100
r3=100
g3=100
b3=100
for j=0 to m-1
for i=0 to n-1 ! da r1,g1,b1 a r2,g2,b2 su equatore al polo r3,g3,b3
Re=r1+j*(r3-r1)/(n-1)+(r2+j*(r3-r2)/(n-1)-r1-j*(r3-r1)/(n-1))/(m-1)*i
Gr=g1+j*(g3-g1)/(n-1)+(g2+j*(g3-g2)/(n-1)-g1-j*(g3-g1)/(n-1))/(m-1)*i
Bu=b1+j*(b3-b1)/(n-1)+(b2+j*(b3-b2)/(n-1)-b1-j*(b3-b1)/(n-1))/(m-1)*i
DEFINE MATERIAL "aij" w,
Re/100,Gr/100,Bu/100
MATERIAL "aij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),sin(j*90/m)!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),sin((j+1)*90/m)!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
!parte superiore lomgitudine 120-240 da blue a red, polo white
r1=not(t)*100
g1=not(t)*100
b1=t*100
r2=t*100
g2=not(t)*100
b2=not(t)*100
r3=100
g3=100
b3=100
for j=0 to m-1
for i=0 to n-1 ! da r1,g1,b1 a r2,g2,b2 su equatore al polo r3,g3,b3
Re=r1+j*(r3-r1)/(n-1)+(r2+j*(r3-r2)/(n-1)-r1-j*(r3-r1)/(n-1))/(m-1)*i
Gr=g1+j*(g3-g1)/(n-1)+(g2+j*(g3-g2)/(n-1)-g1-j*(g3-g1)/(n-1))/(m-1)*i
Bu=b1+j*(b3-b1)/(n-1)+(b2+j*(b3-b2)/(n-1)-b1-j*(b3-b1)/(n-1))/(m-1)*i
DEFINE MATERIAL "bij" w,
Re/100,Gr/100,Bu/100
MATERIAL "bij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),sin(j*90/m)!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),sin((j+1)*90/m)!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
!parte superiore lomgitudine 240-360 da red a green, polo white
r1=t*100
g1=not(t)*100
b1=not(t)*100
r2=not(t)*100
g2=t*100
b2=not(t)*100
r3=100
g3=100
b3=100
for j=0 to m-1
for i=0 to n-1 ! da r1,g1,b1 a r2,g2,b2 su equatore al polo r3,g3,b3
Re=r1+j*(r3-r1)/(n-1)+(r2+j*(r3-r2)/(n-1)-r1-j*(r3-r1)/(n-1))/(m-1)*i
Gr=g1+j*(g3-g1)/(n-1)+(g2+j*(g3-g2)/(n-1)-g1-j*(g3-g1)/(n-1))/(m-1)*i
Bu=b1+j*(b3-b1)/(n-1)+(b2+j*(b3-b2)/(n-1)-b1-j*(b3-b1)/(n-1))/(m-1)*i
DEFINE MATERIAL "cij" w,
Re/100,Gr/100,Bu/100
MATERIAL "cij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),sin(j*90/m)!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),sin((j+1)*90/m)!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
mulz -1
!calotta inferiore lomgitudine 0-120 da green a blue, polo black
r1=not(t)*100
g1=t*100
b1=not(t)*100
r2=not(t)*100
g2=not(t)*100
b2=t*100
r3=0
g3=0
b3=0
for j=0 to m-1
for i=0 to n-1 ! da r1,g1,b1 a r2,g2,b2 su equatore al polo r3,g3,b3
Re=r1+j*(r3-r1)/(n-1)+(r2+j*(r3-r2)/(n-1)-r1-j*(r3-r1)/(n-1))/(m-1)*i
Gr=g1+j*(g3-g1)/(n-1)+(g2+j*(g3-g2)/(n-1)-g1-j*(g3-g1)/(n-1))/(m-1)*i
Bu=b1+j*(b3-b1)/(n-1)+(b2+j*(b3-b2)/(n-1)-b1-j*(b3-b1)/(n-1))/(m-1)*i
DEFINE MATERIAL "dij" w,
Re/100,Gr/100,Bu/100
MATERIAL "dij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),sin(j*90/m)!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),sin((j+1)*90/m)!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
!calotta inferiore lomgitudine 120-240 da blue a red, polo black
r1=not(t)*100
g1=not(t)*100
b1=t*100
r2=t*100
g2=not(t)*100
b2=not(t)*100
r3=0
g3=0
b3=0
for j=0 to m-1
for i=0 to n-1 ! da r1,g1,b1 a r2,g2,b2 su equatore al polo r3,g3,b3
Re=r1+j*(r3-r1)/(n-1)+(r2+j*(r3-r2)/(n-1)-r1-j*(r3-r1)/(n-1))/(m-1)*i
Gr=g1+j*(g3-g1)/(n-1)+(g2+j*(g3-g2)/(n-1)-g1-j*(g3-g1)/(n-1))/(m-1)*i
Bu=b1+j*(b3-b1)/(n-1)+(b2+j*(b3-b2)/(n-1)-b1-j*(b3-b1)/(n-1))/(m-1)*i
DEFINE MATERIAL "eij" w,
Re/100,Gr/100,Bu/100
MATERIAL "eij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),sin(j*90/m)!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),sin((j+1)*90/m)!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
!calotta inferiore lomgitudine 240-360 da red a green, polo black
r1=t*100
g1=not(t)*100
b1=not(t)*100
r2=not(t)*100
g2=t*100
b2=not(t)*100
r3=0
g3=0
b3=0
for j=0 to m-1
for i=0 to n-1 ! da r1,g1,b1 a r2,g2,b2 su equatore al polo r3,g3,b3
Re=r1+j*(r3-r1)/(n-1)+(r2+j*(r3-r2)/(n-1)-r1-j*(r3-r1)/(n-1))/(m-1)*i
Gr=g1+j*(g3-g1)/(n-1)+(g2+j*(g3-g2)/(n-1)-g1-j*(g3-g1)/(n-1))/(m-1)*i
Bu=b1+j*(b3-b1)/(n-1)+(b2+j*(b3-b2)/(n-1)-b1-j*(b3-b1)/(n-1))/(m-1)*i
DEFINE MATERIAL "fij" w,
Re/100,Gr/100,Bu/100
MATERIAL "fij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),sin(j*90/m)!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),sin((j+1)*90/m)!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
del top
Per inserire i valori rgb ai 4 angoli del rettangolo è stata utilizzata la superficie:
z=(z1+(z3-z1)/dy*y)+(z2+(z4-z2)/dy*y-z1-(z3-z1)/dy)/dx*x
che definisce un iperboloide rigato a sella sopra il rettangolo di lati dx e dy che tocca O,
passante per i punti 1:0,0,z1 2:dx,0,z2 4:dx,dy,z4 3:0,dy,z3.
Poichè i valori oscillano entro i limiti, non si creano discontinuità tra i colori.
!!!Istruzioni per ottenere l'oggetto GDL in figura
!Elenco parametri -------------------------------------------:
n=12 !divisoni semimeridiano
m=12 !divisoni lungo equatore
t=0 !bit: =1 RGB, =0 CMYK
p=1 !pen
s="linee in vista" !abc
l="opaco" !abc
!Script parametri -------------------------------------------:
VALUES "s" "linee in vista","colori"
VALUES "l" "opaco","metallo","plastica","vetro","brillante"
! TESTO 2D --------------------------------------------------:
if s="linee in vista" then w=2
if s="colori" then w=3
project2 3,270,w
!TESTO 3D ----------------------------------------------------:
pen p
if l="opaco" then w=2
if l="metallo" then w=3
if l="plastica" then w=4
if l="vetro" then w=5
if l="brillante" then w=6
!parte superiore lomgitudine 0-120 da green a blue, polo white
r1=not(t)*100
g1=t*100
b1=not(t)*100
r2=not(t)*100
g2=not(t)*100
b2=t*100
r3=100
g3=100
b3=100
for j=0 to m-1
for i=0 to n-1 ! da r1,g1,b1 a r2,g2,b2 su equatore al polo r3,g3,b3
Re=r1+j*(r3-r1)/(n-1)+(r2+j*(r3-r2)/(n-1)-r1-j*(r3-r1)/(n-1))/(m-1)*i
Gr=g1+j*(g3-g1)/(n-1)+(g2+j*(g3-g2)/(n-1)-g1-j*(g3-g1)/(n-1))/(m-1)*i
Bu=b1+j*(b3-b1)/(n-1)+(b2+j*(b3-b2)/(n-1)-b1-j*(b3-b1)/(n-1))/(m-1)*i
DEFINE MATERIAL "aij" w,
Re/100,Gr/100,Bu/100
MATERIAL "aij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),sin(j*90/m)!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),sin((j+1)*90/m)!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
!parte superiore lomgitudine 120-240 da blue a red, polo white
r1=not(t)*100
g1=not(t)*100
b1=t*100
r2=t*100
g2=not(t)*100
b2=not(t)*100
r3=100
g3=100
b3=100
for j=0 to m-1
for i=0 to n-1 ! da r1,g1,b1 a r2,g2,b2 su equatore al polo r3,g3,b3
Re=r1+j*(r3-r1)/(n-1)+(r2+j*(r3-r2)/(n-1)-r1-j*(r3-r1)/(n-1))/(m-1)*i
Gr=g1+j*(g3-g1)/(n-1)+(g2+j*(g3-g2)/(n-1)-g1-j*(g3-g1)/(n-1))/(m-1)*i
Bu=b1+j*(b3-b1)/(n-1)+(b2+j*(b3-b2)/(n-1)-b1-j*(b3-b1)/(n-1))/(m-1)*i
DEFINE MATERIAL "bij" w,
Re/100,Gr/100,Bu/100
MATERIAL "bij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),sin(j*90/m)!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),sin((j+1)*90/m)!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
!parte superiore lomgitudine 240-360 da red a green, polo white
r1=t*100
g1=not(t)*100
b1=not(t)*100
r2=not(t)*100
g2=t*100
b2=not(t)*100
r3=100
g3=100
b3=100
for j=0 to m-1
for i=0 to n-1 ! da r1,g1,b1 a r2,g2,b2 su equatore al polo r3,g3,b3
Re=r1+j*(r3-r1)/(n-1)+(r2+j*(r3-r2)/(n-1)-r1-j*(r3-r1)/(n-1))/(m-1)*i
Gr=g1+j*(g3-g1)/(n-1)+(g2+j*(g3-g2)/(n-1)-g1-j*(g3-g1)/(n-1))/(m-1)*i
Bu=b1+j*(b3-b1)/(n-1)+(b2+j*(b3-b2)/(n-1)-b1-j*(b3-b1)/(n-1))/(m-1)*i
DEFINE MATERIAL "cij" w,
Re/100,Gr/100,Bu/100
MATERIAL "cij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),sin(j*90/m)!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),sin((j+1)*90/m)!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
mulz -1
!calotta inferiore lomgitudine 0-120 da green a blue, polo black
r1=not(t)*100
g1=t*100
b1=not(t)*100
r2=not(t)*100
g2=not(t)*100
b2=t*100
r3=0
g3=0
b3=0
for j=0 to m-1
for i=0 to n-1 ! da r1,g1,b1 a r2,g2,b2 su equatore al polo r3,g3,b3
Re=r1+j*(r3-r1)/(n-1)+(r2+j*(r3-r2)/(n-1)-r1-j*(r3-r1)/(n-1))/(m-1)*i
Gr=g1+j*(g3-g1)/(n-1)+(g2+j*(g3-g2)/(n-1)-g1-j*(g3-g1)/(n-1))/(m-1)*i
Bu=b1+j*(b3-b1)/(n-1)+(b2+j*(b3-b2)/(n-1)-b1-j*(b3-b1)/(n-1))/(m-1)*i
DEFINE MATERIAL "dij" w,
Re/100,Gr/100,Bu/100
MATERIAL "dij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),sin(j*90/m)!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),sin((j+1)*90/m)!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
!calotta inferiore lomgitudine 120-240 da blue a red, polo black
r1=not(t)*100
g1=not(t)*100
b1=t*100
r2=t*100
g2=not(t)*100
b2=not(t)*100
r3=0
g3=0
b3=0
for j=0 to m-1
for i=0 to n-1 ! da r1,g1,b1 a r2,g2,b2 su equatore al polo r3,g3,b3
Re=r1+j*(r3-r1)/(n-1)+(r2+j*(r3-r2)/(n-1)-r1-j*(r3-r1)/(n-1))/(m-1)*i
Gr=g1+j*(g3-g1)/(n-1)+(g2+j*(g3-g2)/(n-1)-g1-j*(g3-g1)/(n-1))/(m-1)*i
Bu=b1+j*(b3-b1)/(n-1)+(b2+j*(b3-b2)/(n-1)-b1-j*(b3-b1)/(n-1))/(m-1)*i
DEFINE MATERIAL "eij" w,
Re/100,Gr/100,Bu/100
MATERIAL "eij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),sin(j*90/m)!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),sin((j+1)*90/m)!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
!calotta inferiore lomgitudine 240-360 da red a green, polo black
r1=t*100
g1=not(t)*100
b1=not(t)*100
r2=not(t)*100
g2=t*100
b2=not(t)*100
r3=0
g3=0
b3=0
for j=0 to m-1
for i=0 to n-1 ! da r1,g1,b1 a r2,g2,b2 su equatore al polo r3,g3,b3
Re=r1+j*(r3-r1)/(n-1)+(r2+j*(r3-r2)/(n-1)-r1-j*(r3-r1)/(n-1))/(m-1)*i
Gr=g1+j*(g3-g1)/(n-1)+(g2+j*(g3-g2)/(n-1)-g1-j*(g3-g1)/(n-1))/(m-1)*i
Bu=b1+j*(b3-b1)/(n-1)+(b2+j*(b3-b2)/(n-1)-b1-j*(b3-b1)/(n-1))/(m-1)*i
DEFINE MATERIAL "fij" w,
Re/100,Gr/100,Bu/100
MATERIAL "fij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),sin(j*90/m)!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),sin((j+1)*90/m)!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
del top

Anonymous
Not applicable
Options
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
2012-09-19 05:03 PM
2012-09-19
05:03 PM
In questo caso a sfera dei colori non comprende solo la buccia con primari e secondari, ma anche i colori terziari che andando verso il centro perdono la saturazione formando il grigio medio.
Un colore che sulla buccia vale r,g,b, passando lungo il diametro,
si trasforma dalla parte opposta in 100-r,100-g,100-b.
Pertanto se il raggio della sfera è 1, alla distanza x dal centro sfera il colore sarà:
(r-50)*x+50,(g-50)*x+50,(b-50)*x+50
che per x=1 dà r,g,b e per x=-1 dà 100-r,100-g,100-b
Nell'esempio il raggio della sfera rimane invariato,
mentre diminuisce solo la saturazione diminuendo x in percentuale,
fino a 0 per grigio medio.
In pratica le infinite sfere concentriche qui vengono rappresentate da una unica sfera. Aumentando x da 0 a 100 si passa dal centro alla buccia (massima saturazione)
!!!Istruzioni per ottenere l'oggetto GDL in figura
!Elenco parametri -------------------------------------------:
n=10 !divisoni semimeridiano
m=10 !divisoni lungo equatore
t=0 !bit: =1 RGB, =0 CMYK
p=1 !pen
s="linee in vista" !abc
l="opaco" !abc
x=50 !saturazione
o=1 !mostra facce in 2D
!Script parametri -------------------------------------------:
VALUES "s" "linee in vista","colori"
VALUES "l" "opaco","metallo","plastica","vetro","brillante"
! TESTO 2D --------------------------------------------------:
if s="linee in vista" then w=2
if s="colori" then w=3
if o=1 then project2 3,270,w
if o=0 then circle2 0,0,1
!TESTO 3D ----------------------------------------------------:
pen p
if l="opaco" then w=2
if l="metallo" then w=3
if l="plastica" then w=4
if l="vetro" then w=5
if l="brillante" then w=6
!parte superiore lomgitudine 0-120 da green a blue, polo white
r1=not(t)*100
g1=t*100
b1=not(t)*100
r2=not(t)*100
g2=not(t)*100
b2=t*100
r3=100
g3=100
b3=100
for j=0 to m-1
for i=0 to n-1
Re=((r1-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1)+(((r2-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r2-50)*x/100+50))/(n-1)-((r1-50)*x/100+50)-j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1))/(m-1)*i
Gr=((g1-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1)+(((g2-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g2-50)*x/100+50))/(n-1)-((g1-50)*x/100+50)-j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1))/(m-1)*i
Bu=((b1-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1)+(((b2-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b2-50)*x/100+50))/(n-1)-((b1-50)*x/100+50)-j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1))/(m-1)*i
DEFINE MATERIAL "aij" w,
Re/100,Gr/100,Bu/100
MATERIAL "aij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),sin(j*90/m)!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),sin((j+1)*90/m)!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
!parte superiore lomgitudine 120-240 da blue a red, polo white
r1=not(t)*100
g1=not(t)*100
b1=t*100
r2=t*100
g2=not(t)*100
b2=not(t)*100
r3=100
g3=100
b3=100
for j=0 to m-1
for i=0 to n-1
Re=((r1-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1)+(((r2-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r2-50)*x/100+50))/(n-1)-((r1-50)*x/100+50)-j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1))/(m-1)*i
Gr=((g1-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1)+(((g2-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g2-50)*x/100+50))/(n-1)-((g1-50)*x/100+50)-j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1))/(m-1)*i
Bu=((b1-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1)+(((b2-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b2-50)*x/100+50))/(n-1)-((b1-50)*x/100+50)-j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1))/(m-1)*i
DEFINE MATERIAL "bij" w,
Re/100,Gr/100,Bu/100
MATERIAL "bij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),sin(j*90/m)!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),sin((j+1)*90/m)!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
!parte superiore lomgitudine 240-360 da red a green, polo white
r1=t*100
g1=not(t)*100
b1=not(t)*100
r2=not(t)*100
g2=t*100
b2=not(t)*100
r3=100
g3=100
b3=100
for j=0 to m-1
for i=0 to n-1
Re=((r1-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1)+(((r2-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r2-50)*x/100+50))/(n-1)-((r1-50)*x/100+50)-j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1))/(m-1)*i
Gr=((g1-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1)+(((g2-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g2-50)*x/100+50))/(n-1)-((g1-50)*x/100+50)-j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1))/(m-1)*i
Bu=((b1-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1)+(((b2-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b2-50)*x/100+50))/(n-1)-((b1-50)*x/100+50)-j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1))/(m-1)*i
DEFINE MATERIAL "cij" w,
Re/100,Gr/100,Bu/100
MATERIAL "cij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),sin(j*90/m)!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),sin((j+1)*90/m)!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
mulz -1
!calotta inferiore lomgitudine 0-120 da green a blue, polo black
r1=not(t)*100
g1=t*100
b1=not(t)*100
r2=not(t)*100
g2=not(t)*100
b2=t*100
r3=0
g3=0
b3=0
for j=0 to m-1
for i=0 to n-1
Re=((r1-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1)+(((r2-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r2-50)*x/100+50))/(n-1)-((r1-50)*x/100+50)-j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1))/(m-1)*i
Gr=((g1-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1)+(((g2-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g2-50)*x/100+50))/(n-1)-((g1-50)*x/100+50)-j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1))/(m-1)*i
Bu=((b1-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1)+(((b2-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b2-50)*x/100+50))/(n-1)-((b1-50)*x/100+50)-j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1))/(m-1)*i
DEFINE MATERIAL "dij" w,
Re/100,Gr/100,Bu/100
MATERIAL "dij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),sin(j*90/m)!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),sin((j+1)*90/m)!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
!calotta inferiore lomgitudine 120-240 da blue a red, polo black
r1=not(t)*100
g1=not(t)*100
b1=t*100
r2=t*100
g2=not(t)*100
b2=not(t)*100
r3=0
b3=0
g3=0
for j=0 to m-1
for i=0 to n-1
Re=((r1-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1)+(((r2-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r2-50)*x/100+50))/(n-1)-((r1-50)*x/100+50)-j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1))/(m-1)*i
Gr=((g1-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1)+(((g2-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g2-50)*x/100+50))/(n-1)-((g1-50)*x/100+50)-j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1))/(m-1)*i
Bu=((b1-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1)+(((b2-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b2-50)*x/100+50))/(n-1)-((b1-50)*x/100+50)-j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1))/(m-1)*i
DEFINE MATERIAL "eij" w,
Re/100,Gr/100,Bu/100
MATERIAL "eij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),sin(j*90/m)!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),sin((j+1)*90/m)!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
!calotta inferiore lomgitudine 240-360 da red a green, polo black
r1=t*100
g1=not(t)*100
b1=not(t)*100
r2=not(t)*100
g2=t*100
b2=not(t)*100
r3=0
b3=0
g3=0
for j=0 to m-1
for i=0 to n-1
Re=((r1-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1)+(((r2-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r2-50)*x/100+50))/(n-1)-((r1-50)*x/100+50)-j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1))/(m-1)*i
Gr=((g1-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1)+(((g2-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g2-50)*x/100+50))/(n-1)-((g1-50)*x/100+50)-j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1))/(m-1)*i
Bu=((b1-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1)+(((b2-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b2-50)*x/100+50))/(n-1)-((b1-50)*x/100+50)-j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1))/(m-1)*i
DEFINE MATERIAL "fij" w,
Re/100,Gr/100,Bu/100
MATERIAL "fij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),sin(j*90/m)!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),sin((j+1)*90/m)!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
!del 6, ntr()-5 cancella i soli movimenti usati per costruire la sfera
del top
Un colore che sulla buccia vale r,g,b, passando lungo il diametro,
si trasforma dalla parte opposta in 100-r,100-g,100-b.
Pertanto se il raggio della sfera è 1, alla distanza x dal centro sfera il colore sarà:
(r-50)*x+50,(g-50)*x+50,(b-50)*x+50
che per x=1 dà r,g,b e per x=-1 dà 100-r,100-g,100-b
Nell'esempio il raggio della sfera rimane invariato,
mentre diminuisce solo la saturazione diminuendo x in percentuale,
fino a 0 per grigio medio.
In pratica le infinite sfere concentriche qui vengono rappresentate da una unica sfera. Aumentando x da 0 a 100 si passa dal centro alla buccia (massima saturazione)
!!!Istruzioni per ottenere l'oggetto GDL in figura
!Elenco parametri -------------------------------------------:
n=10 !divisoni semimeridiano
m=10 !divisoni lungo equatore
t=0 !bit: =1 RGB, =0 CMYK
p=1 !pen
s="linee in vista" !abc
l="opaco" !abc
x=50 !saturazione
o=1 !mostra facce in 2D
!Script parametri -------------------------------------------:
VALUES "s" "linee in vista","colori"
VALUES "l" "opaco","metallo","plastica","vetro","brillante"
! TESTO 2D --------------------------------------------------:
if s="linee in vista" then w=2
if s="colori" then w=3
if o=1 then project2 3,270,w
if o=0 then circle2 0,0,1
!TESTO 3D ----------------------------------------------------:
pen p
if l="opaco" then w=2
if l="metallo" then w=3
if l="plastica" then w=4
if l="vetro" then w=5
if l="brillante" then w=6
!parte superiore lomgitudine 0-120 da green a blue, polo white
r1=not(t)*100
g1=t*100
b1=not(t)*100
r2=not(t)*100
g2=not(t)*100
b2=t*100
r3=100
g3=100
b3=100
for j=0 to m-1
for i=0 to n-1
Re=((r1-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1)+(((r2-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r2-50)*x/100+50))/(n-1)-((r1-50)*x/100+50)-j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1))/(m-1)*i
Gr=((g1-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1)+(((g2-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g2-50)*x/100+50))/(n-1)-((g1-50)*x/100+50)-j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1))/(m-1)*i
Bu=((b1-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1)+(((b2-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b2-50)*x/100+50))/(n-1)-((b1-50)*x/100+50)-j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1))/(m-1)*i
DEFINE MATERIAL "aij" w,
Re/100,Gr/100,Bu/100
MATERIAL "aij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),sin(j*90/m)!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),sin((j+1)*90/m)!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
!parte superiore lomgitudine 120-240 da blue a red, polo white
r1=not(t)*100
g1=not(t)*100
b1=t*100
r2=t*100
g2=not(t)*100
b2=not(t)*100
r3=100
g3=100
b3=100
for j=0 to m-1
for i=0 to n-1
Re=((r1-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1)+(((r2-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r2-50)*x/100+50))/(n-1)-((r1-50)*x/100+50)-j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1))/(m-1)*i
Gr=((g1-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1)+(((g2-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g2-50)*x/100+50))/(n-1)-((g1-50)*x/100+50)-j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1))/(m-1)*i
Bu=((b1-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1)+(((b2-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b2-50)*x/100+50))/(n-1)-((b1-50)*x/100+50)-j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1))/(m-1)*i
DEFINE MATERIAL "bij" w,
Re/100,Gr/100,Bu/100
MATERIAL "bij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),sin(j*90/m)!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),sin((j+1)*90/m)!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
!parte superiore lomgitudine 240-360 da red a green, polo white
r1=t*100
g1=not(t)*100
b1=not(t)*100
r2=not(t)*100
g2=t*100
b2=not(t)*100
r3=100
g3=100
b3=100
for j=0 to m-1
for i=0 to n-1
Re=((r1-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1)+(((r2-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r2-50)*x/100+50))/(n-1)-((r1-50)*x/100+50)-j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1))/(m-1)*i
Gr=((g1-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1)+(((g2-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g2-50)*x/100+50))/(n-1)-((g1-50)*x/100+50)-j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1))/(m-1)*i
Bu=((b1-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1)+(((b2-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b2-50)*x/100+50))/(n-1)-((b1-50)*x/100+50)-j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1))/(m-1)*i
DEFINE MATERIAL "cij" w,
Re/100,Gr/100,Bu/100
MATERIAL "cij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),sin(j*90/m)!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),sin((j+1)*90/m)!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
mulz -1
!calotta inferiore lomgitudine 0-120 da green a blue, polo black
r1=not(t)*100
g1=t*100
b1=not(t)*100
r2=not(t)*100
g2=not(t)*100
b2=t*100
r3=0
g3=0
b3=0
for j=0 to m-1
for i=0 to n-1
Re=((r1-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1)+(((r2-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r2-50)*x/100+50))/(n-1)-((r1-50)*x/100+50)-j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1))/(m-1)*i
Gr=((g1-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1)+(((g2-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g2-50)*x/100+50))/(n-1)-((g1-50)*x/100+50)-j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1))/(m-1)*i
Bu=((b1-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1)+(((b2-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b2-50)*x/100+50))/(n-1)-((b1-50)*x/100+50)-j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1))/(m-1)*i
DEFINE MATERIAL "dij" w,
Re/100,Gr/100,Bu/100
MATERIAL "dij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),sin(j*90/m)!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),sin((j+1)*90/m)!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
!calotta inferiore lomgitudine 120-240 da blue a red, polo black
r1=not(t)*100
g1=not(t)*100
b1=t*100
r2=t*100
g2=not(t)*100
b2=not(t)*100
r3=0
b3=0
g3=0
for j=0 to m-1
for i=0 to n-1
Re=((r1-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1)+(((r2-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r2-50)*x/100+50))/(n-1)-((r1-50)*x/100+50)-j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1))/(m-1)*i
Gr=((g1-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1)+(((g2-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g2-50)*x/100+50))/(n-1)-((g1-50)*x/100+50)-j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1))/(m-1)*i
Bu=((b1-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1)+(((b2-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b2-50)*x/100+50))/(n-1)-((b1-50)*x/100+50)-j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1))/(m-1)*i
DEFINE MATERIAL "eij" w,
Re/100,Gr/100,Bu/100
MATERIAL "eij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),sin(j*90/m)!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),sin((j+1)*90/m)!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
!calotta inferiore lomgitudine 240-360 da red a green, polo black
r1=t*100
g1=not(t)*100
b1=not(t)*100
r2=not(t)*100
g2=t*100
b2=not(t)*100
r3=0
b3=0
g3=0
for j=0 to m-1
for i=0 to n-1
Re=((r1-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1)+(((r2-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r2-50)*x/100+50))/(n-1)-((r1-50)*x/100+50)-j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1))/(m-1)*i
Gr=((g1-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1)+(((g2-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g2-50)*x/100+50))/(n-1)-((g1-50)*x/100+50)-j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1))/(m-1)*i
Bu=((b1-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1)+(((b2-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b2-50)*x/100+50))/(n-1)-((b1-50)*x/100+50)-j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1))/(m-1)*i
DEFINE MATERIAL "fij" w,
Re/100,Gr/100,Bu/100
MATERIAL "fij"
base
vert cos(j*90/m)*cos(i*120/n),cos(j*90/m)*sin(i*120/n),sin(j*90/m)!1
vert cos(j*90/m)*cos((i+1)*120/n),cos(j*90/m)*sin((i+1)*120/n),sin(j*90/m)!2
vert cos((j+1)*90/m)*cos((i+1)*120/n),cos((j+1)*90/m)*sin((i+1)*120/n),sin((j+1)*90/m)!3
vert cos((j+1)*90/m)*cos(i*120/n),cos((j+1)*90/m)*sin(i*120/n),sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
!del 6, ntr()-5 cancella i soli movimenti usati per costruire la sfera
del top
Anonymous
Not applicable
Options
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
2012-09-19 05:36 PM
2012-09-19
05:36 PM
La sfera dei colori non comprende solo la buccia con primari e secondari, ma anche i colori terziari che andando verso il centro perdono la saturazione formando il grigio medio.
Un colore che sulla buccia vale r,g,b, passando lungo il diametro,
si trasforma dalla parte opposta in 100-r,100-g,100-b.
Pertanto se il raggio della sfera è 1, alla distanza x dal centro sfera il colore sarà:
(r-50)*x+50,(g-50)*x+50,(b-50)*x+50
che per x=1 dà r,g,b e per x=-1 dà 100-r,100-g,100-b
Nell'esempio, per mostrare le sfere interne, sono state disposte in sequenza.
In teoria le sfere più piccole si ingrigiscono, pur essendo
l'effetto poco evidente in 3D.
Le sfere andrebbero immaginate una dentro all'altra con unico centro.
!!!Istruzioni per ottenere l'oggetto GDL in figura
!Elenco parametri -------------------------------------------:
n=10 !divisoni semimeridiano
m=10 !divisoni lungo equatore
t=0 !bit: =1 RGB, =0 CMYK
p=1 !pen
s="linee in vista" !abc
l="opaco" !abc
g="Top view" !abc
o=1 !mostra facce in 2D
!Script parametri -------------------------------------------:
VALUES "s" "linee in vista","colori"
VALUES "l" "opaco","metallo","plastica","vetro","brillante"
VALUES "g" "Top view","Side view","Frontal axonometry",
"Isometric axonometry","Monometric axonometry","Dimetric axonometry"
! TESTO 2D --------------------------------------------------:
if g="Top view" then pr=3
if g="Side view" then pr=4
if g="Frontal axonometry" then pr=6
if g="Isometric axonometry" then pr=7
if g="Monometric axonometry" then pr=8
if g="Dimetric axonometry" then pr=9
if s="linee in vista" then w=2
if s="colori" then w=3
project2 pr,270,w
!TESTO 3D----------------------------------------------------:
pen p
x=100
gosub 1
n=8
m=8
addx 1.8
x=80
gosub 1
n=6
m=6
addx 1.4
x=60
gosub 1
n=4
m=4
addx 1
x=40
gosub 1
n=2
m=2
addx 0.6
x=20
gosub 1
del top
end
1: if l="opaco" then w=2
if l="metallo" then w=3
if l="plastica" then w=4
if l="vetro" then w=5
if l="brillante" then w=6
!parte superiore lomgitudine 0-120 da green a blue, polo white
r1=not(t)*100
g1=t*100
b1=not(t)*100
r2=not(t)*100
g2=not(t)*100
b2=t*100
r3=100
g3=100
b3=100
for j=0 to m-1
for i=0 to n-1 ! da ((r1-50)*x/100+50),((g1-50)*x/100+50),((b1-50)*x/100+50) a ((r2-50)*x/100+50),((g2-50)*x/100+50),((b2-50)*x/100+50) (riga in basso) e da ((r3-50)*x/100+50),((g3-50)*x/100+50),((b3-50)*x/100+50) a a r4,g4,b4 (riga in alto)
Re=((r1-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1)+(((r2-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r2-50)*x/100+50))/(n-1)-((r1-50)*x/100+50)-j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1))/(m-1)*i
Gr=((g1-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1)+(((g2-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g2-50)*x/100+50))/(n-1)-((g1-50)*x/100+50)-j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1))/(m-1)*i
Bu=((b1-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1)+(((b2-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b2-50)*x/100+50))/(n-1)-((b1-50)*x/100+50)-j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1))/(m-1)*i
DEFINE MATERIAL "aij" w,
Re/100,Gr/100,Bu/100
MATERIAL "aij"
base
vert x/100*cos(j*90/m)*cos(i*120/n),x/100*cos(j*90/m)*sin(i*120/n),x/100*sin(j*90/m)!1
vert x/100*cos(j*90/m)*cos((i+1)*120/n),x/100*cos(j*90/m)*sin((i+1)*120/n),x/100*sin(j*90/m)!2
vert x/100*cos((j+1)*90/m)*cos((i+1)*120/n),x/100*cos((j+1)*90/m)*sin((i+1)*120/n),x/100*sin((j+1)*90/m)!3
vert x/100*cos((j+1)*90/m)*cos(i*120/n),x/100*cos((j+1)*90/m)*sin(i*120/n),x/100*sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
!parte superiore lomgitudine 120-240 da blue a red, polo white
r1=not(t)*100
g1=not(t)*100
b1=t*100
r2=t*100
g2=not(t)*100
b2=not(t)*100
r3=100
g3=100
b3=100
for j=0 to m-1
for i=0 to n-1 ! da ((r1-50)*x/100+50),((g1-50)*x/100+50),((b1-50)*x/100+50) a ((r2-50)*x/100+50),((g2-50)*x/100+50),((b2-50)*x/100+50) (riga in basso) e da ((r3-50)*x/100+50),((g3-50)*x/100+50),((b3-50)*x/100+50) a a r4,g4,b4 (riga in alto)
Re=((r1-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1)+(((r2-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r2-50)*x/100+50))/(n-1)-((r1-50)*x/100+50)-j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1))/(m-1)*i
Gr=((g1-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1)+(((g2-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g2-50)*x/100+50))/(n-1)-((g1-50)*x/100+50)-j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1))/(m-1)*i
Bu=((b1-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1)+(((b2-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b2-50)*x/100+50))/(n-1)-((b1-50)*x/100+50)-j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1))/(m-1)*i
DEFINE MATERIAL "bij" w,
Re/100,Gr/100,Bu/100
MATERIAL "bij"
base
vert x/100*cos(j*90/m)*cos(i*120/n),x/100*cos(j*90/m)*sin(i*120/n),x/100*sin(j*90/m)!1
vert x/100*cos(j*90/m)*cos((i+1)*120/n),x/100*cos(j*90/m)*sin((i+1)*120/n),x/100*sin(j*90/m)!2
vert x/100*cos((j+1)*90/m)*cos((i+1)*120/n),x/100*cos((j+1)*90/m)*sin((i+1)*120/n),x/100*sin((j+1)*90/m)!3
vert x/100*cos((j+1)*90/m)*cos(i*120/n),x/100*cos((j+1)*90/m)*sin(i*120/n),x/100*sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
!parte superiore lomgitudine 240-360 da red a green, polo white
r1=t*100
g1=not(t)*100
b1=not(t)*100
r2=not(t)*100
g2=t*100
b2=not(t)*100
r3=100
g3=100
b3=100
for j=0 to m-1
for i=0 to n-1 ! da ((r1-50)*x/100+50),((g1-50)*x/100+50),((b1-50)*x/100+50) a ((r2-50)*x/100+50),((g2-50)*x/100+50),((b2-50)*x/100+50) (riga in basso) e da ((r3-50)*x/100+50),((g3-50)*x/100+50),((b3-50)*x/100+50) a a r4,g4,b4 (riga in alto)
Re=((r1-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1)+(((r2-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r2-50)*x/100+50))/(n-1)-((r1-50)*x/100+50)-j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1))/(m-1)*i
Gr=((g1-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1)+(((g2-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g2-50)*x/100+50))/(n-1)-((g1-50)*x/100+50)-j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1))/(m-1)*i
Bu=((b1-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1)+(((b2-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b2-50)*x/100+50))/(n-1)-((b1-50)*x/100+50)-j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1))/(m-1)*i
DEFINE MATERIAL "cij" w,
Re/100,Gr/100,Bu/100
MATERIAL "cij"
base
vert x/100*cos(j*90/m)*cos(i*120/n),x/100*cos(j*90/m)*sin(i*120/n),x/100*sin(j*90/m)!1
vert x/100*cos(j*90/m)*cos((i+1)*120/n),x/100*cos(j*90/m)*sin((i+1)*120/n),x/100*sin(j*90/m)!2
vert x/100*cos((j+1)*90/m)*cos((i+1)*120/n),x/100*cos((j+1)*90/m)*sin((i+1)*120/n),x/100*sin((j+1)*90/m)!3
vert x/100*cos((j+1)*90/m)*cos(i*120/n),x/100*cos((j+1)*90/m)*sin(i*120/n),x/100*sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
mulz -1
!calotta inferiore lomgitudine 0-120 da green a blue, polo black
r1=not(t)*100
g1=t*100
b1=not(t)*100
r2=not(t)*100
g2=not(t)*100
b2=t*100
r3=0
g3=0
b3=0
for j=0 to m-1
for i=0 to n-1 ! da ((r1-50)*x/100+50),((g1-50)*x/100+50),((b1-50)*x/100+50) a ((r2-50)*x/100+50),((g2-50)*x/100+50),((b2-50)*x/100+50) (riga in basso) e da ((r3-50)*x/100+50),((g3-50)*x/100+50),((b3-50)*x/100+50) a a r4,g4,b4 (riga in alto)
Re=((r1-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1)+(((r2-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r2-50)*x/100+50))/(n-1)-((r1-50)*x/100+50)-j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1))/(m-1)*i
Gr=((g1-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1)+(((g2-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g2-50)*x/100+50))/(n-1)-((g1-50)*x/100+50)-j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1))/(m-1)*i
Bu=((b1-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1)+(((b2-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b2-50)*x/100+50))/(n-1)-((b1-50)*x/100+50)-j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1))/(m-1)*i
DEFINE MATERIAL "dij" w,
Re/100,Gr/100,Bu/100
MATERIAL "dij"
base
vert x/100*cos(j*90/m)*cos(i*120/n),x/100*cos(j*90/m)*sin(i*120/n),x/100*sin(j*90/m)!1
vert x/100*cos(j*90/m)*cos((i+1)*120/n),x/100*cos(j*90/m)*sin((i+1)*120/n),x/100*sin(j*90/m)!2
vert x/100*cos((j+1)*90/m)*cos((i+1)*120/n),x/100*cos((j+1)*90/m)*sin((i+1)*120/n),x/100*sin((j+1)*90/m)!3
vert x/100*cos((j+1)*90/m)*cos(i*120/n),x/100*cos((j+1)*90/m)*sin(i*120/n),x/100*sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
!calotta inferiore lomgitudine 120-240 da blue a red, polo black
r1=not(t)*100
g1=not(t)*100
b1=t*100
r2=t*100
g2=not(t)*100
b2=not(t)*100
r3=0
b3=0
g3=0
for j=0 to m-1
for i=0 to n-1 ! da ((r1-50)*x/100+50),((g1-50)*x/100+50),((b1-50)*x/100+50) a ((r2-50)*x/100+50),((g2-50)*x/100+50),((b2-50)*x/100+50) (riga in basso) e da ((r3-50)*x/100+50),((g3-50)*x/100+50),((b3-50)*x/100+50) a a r4,g4,b4 (riga in alto)
Re=((r1-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1)+(((r2-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r2-50)*x/100+50))/(n-1)-((r1-50)*x/100+50)-j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1))/(m-1)*i
Gr=((g1-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1)+(((g2-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g2-50)*x/100+50))/(n-1)-((g1-50)*x/100+50)-j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1))/(m-1)*i
Bu=((b1-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1)+(((b2-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b2-50)*x/100+50))/(n-1)-((b1-50)*x/100+50)-j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1))/(m-1)*i
DEFINE MATERIAL "eij" w,
Re/100,Gr/100,Bu/100
MATERIAL "eij"
base
vert x/100*cos(j*90/m)*cos(i*120/n),x/100*cos(j*90/m)*sin(i*120/n),x/100*sin(j*90/m)!1
vert x/100*cos(j*90/m)*cos((i+1)*120/n),x/100*cos(j*90/m)*sin((i+1)*120/n),x/100*sin(j*90/m)!2
vert x/100*cos((j+1)*90/m)*cos((i+1)*120/n),x/100*cos((j+1)*90/m)*sin((i+1)*120/n),x/100*sin((j+1)*90/m)!3
vert x/100*cos((j+1)*90/m)*cos(i*120/n),x/100*cos((j+1)*90/m)*sin(i*120/n),x/100*sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
!calotta inferiore lomgitudine 240-360 da red a green, polo black
r1=t*100
g1=not(t)*100
b1=not(t)*100
r2=not(t)*100
g2=t*100
b2=not(t)*100
r3=0
b3=0
g3=0
for j=0 to m-1
for i=0 to n-1 ! da ((r1-50)*x/100+50),((g1-50)*x/100+50),((b1-50)*x/100+50) a ((r2-50)*x/100+50),((g2-50)*x/100+50),((b2-50)*x/100+50) (riga in basso) e da ((r3-50)*x/100+50),((g3-50)*x/100+50),((b3-50)*x/100+50) a a r4,g4,b4 (riga in alto)
Re=((r1-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1)+(((r2-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r2-50)*x/100+50))/(n-1)-((r1-50)*x/100+50)-j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1))/(m-1)*i
Gr=((g1-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1)+(((g2-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g2-50)*x/100+50))/(n-1)-((g1-50)*x/100+50)-j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1))/(m-1)*i
Bu=((b1-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1)+(((b2-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b2-50)*x/100+50))/(n-1)-((b1-50)*x/100+50)-j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1))/(m-1)*i
DEFINE MATERIAL "fij" w,
Re/100,Gr/100,Bu/100
MATERIAL "fij"
base
vert x/100*cos(j*90/m)*cos(i*120/n),x/100*cos(j*90/m)*sin(i*120/n),x/100*sin(j*90/m)!1
vert x/100*cos(j*90/m)*cos((i+1)*120/n),x/100*cos(j*90/m)*sin((i+1)*120/n),x/100*sin(j*90/m)!2
vert x/100*cos((j+1)*90/m)*cos((i+1)*120/n),x/100*cos((j+1)*90/m)*sin((i+1)*120/n),x/100*sin((j+1)*90/m)!3
vert x/100*cos((j+1)*90/m)*cos(i*120/n),x/100*cos((j+1)*90/m)*sin(i*120/n),x/100*sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
del 6, ntr()-5
return

Un colore che sulla buccia vale r,g,b, passando lungo il diametro,
si trasforma dalla parte opposta in 100-r,100-g,100-b.
Pertanto se il raggio della sfera è 1, alla distanza x dal centro sfera il colore sarà:
(r-50)*x+50,(g-50)*x+50,(b-50)*x+50
che per x=1 dà r,g,b e per x=-1 dà 100-r,100-g,100-b
Nell'esempio, per mostrare le sfere interne, sono state disposte in sequenza.
In teoria le sfere più piccole si ingrigiscono, pur essendo
l'effetto poco evidente in 3D.
Le sfere andrebbero immaginate una dentro all'altra con unico centro.
!!!Istruzioni per ottenere l'oggetto GDL in figura
!Elenco parametri -------------------------------------------:
n=10 !divisoni semimeridiano
m=10 !divisoni lungo equatore
t=0 !bit: =1 RGB, =0 CMYK
p=1 !pen
s="linee in vista" !abc
l="opaco" !abc
g="Top view" !abc
o=1 !mostra facce in 2D
!Script parametri -------------------------------------------:
VALUES "s" "linee in vista","colori"
VALUES "l" "opaco","metallo","plastica","vetro","brillante"
VALUES "g" "Top view","Side view","Frontal axonometry",
"Isometric axonometry","Monometric axonometry","Dimetric axonometry"
! TESTO 2D --------------------------------------------------:
if g="Top view" then pr=3
if g="Side view" then pr=4
if g="Frontal axonometry" then pr=6
if g="Isometric axonometry" then pr=7
if g="Monometric axonometry" then pr=8
if g="Dimetric axonometry" then pr=9
if s="linee in vista" then w=2
if s="colori" then w=3
project2 pr,270,w
!TESTO 3D----------------------------------------------------:
pen p
x=100
gosub 1
n=8
m=8
addx 1.8
x=80
gosub 1
n=6
m=6
addx 1.4
x=60
gosub 1
n=4
m=4
addx 1
x=40
gosub 1
n=2
m=2
addx 0.6
x=20
gosub 1
del top
end
1: if l="opaco" then w=2
if l="metallo" then w=3
if l="plastica" then w=4
if l="vetro" then w=5
if l="brillante" then w=6
!parte superiore lomgitudine 0-120 da green a blue, polo white
r1=not(t)*100
g1=t*100
b1=not(t)*100
r2=not(t)*100
g2=not(t)*100
b2=t*100
r3=100
g3=100
b3=100
for j=0 to m-1
for i=0 to n-1 ! da ((r1-50)*x/100+50),((g1-50)*x/100+50),((b1-50)*x/100+50) a ((r2-50)*x/100+50),((g2-50)*x/100+50),((b2-50)*x/100+50) (riga in basso) e da ((r3-50)*x/100+50),((g3-50)*x/100+50),((b3-50)*x/100+50) a a r4,g4,b4 (riga in alto)
Re=((r1-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1)+(((r2-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r2-50)*x/100+50))/(n-1)-((r1-50)*x/100+50)-j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1))/(m-1)*i
Gr=((g1-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1)+(((g2-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g2-50)*x/100+50))/(n-1)-((g1-50)*x/100+50)-j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1))/(m-1)*i
Bu=((b1-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1)+(((b2-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b2-50)*x/100+50))/(n-1)-((b1-50)*x/100+50)-j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1))/(m-1)*i
DEFINE MATERIAL "aij" w,
Re/100,Gr/100,Bu/100
MATERIAL "aij"
base
vert x/100*cos(j*90/m)*cos(i*120/n),x/100*cos(j*90/m)*sin(i*120/n),x/100*sin(j*90/m)!1
vert x/100*cos(j*90/m)*cos((i+1)*120/n),x/100*cos(j*90/m)*sin((i+1)*120/n),x/100*sin(j*90/m)!2
vert x/100*cos((j+1)*90/m)*cos((i+1)*120/n),x/100*cos((j+1)*90/m)*sin((i+1)*120/n),x/100*sin((j+1)*90/m)!3
vert x/100*cos((j+1)*90/m)*cos(i*120/n),x/100*cos((j+1)*90/m)*sin(i*120/n),x/100*sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
!parte superiore lomgitudine 120-240 da blue a red, polo white
r1=not(t)*100
g1=not(t)*100
b1=t*100
r2=t*100
g2=not(t)*100
b2=not(t)*100
r3=100
g3=100
b3=100
for j=0 to m-1
for i=0 to n-1 ! da ((r1-50)*x/100+50),((g1-50)*x/100+50),((b1-50)*x/100+50) a ((r2-50)*x/100+50),((g2-50)*x/100+50),((b2-50)*x/100+50) (riga in basso) e da ((r3-50)*x/100+50),((g3-50)*x/100+50),((b3-50)*x/100+50) a a r4,g4,b4 (riga in alto)
Re=((r1-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1)+(((r2-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r2-50)*x/100+50))/(n-1)-((r1-50)*x/100+50)-j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1))/(m-1)*i
Gr=((g1-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1)+(((g2-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g2-50)*x/100+50))/(n-1)-((g1-50)*x/100+50)-j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1))/(m-1)*i
Bu=((b1-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1)+(((b2-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b2-50)*x/100+50))/(n-1)-((b1-50)*x/100+50)-j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1))/(m-1)*i
DEFINE MATERIAL "bij" w,
Re/100,Gr/100,Bu/100
MATERIAL "bij"
base
vert x/100*cos(j*90/m)*cos(i*120/n),x/100*cos(j*90/m)*sin(i*120/n),x/100*sin(j*90/m)!1
vert x/100*cos(j*90/m)*cos((i+1)*120/n),x/100*cos(j*90/m)*sin((i+1)*120/n),x/100*sin(j*90/m)!2
vert x/100*cos((j+1)*90/m)*cos((i+1)*120/n),x/100*cos((j+1)*90/m)*sin((i+1)*120/n),x/100*sin((j+1)*90/m)!3
vert x/100*cos((j+1)*90/m)*cos(i*120/n),x/100*cos((j+1)*90/m)*sin(i*120/n),x/100*sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
!parte superiore lomgitudine 240-360 da red a green, polo white
r1=t*100
g1=not(t)*100
b1=not(t)*100
r2=not(t)*100
g2=t*100
b2=not(t)*100
r3=100
g3=100
b3=100
for j=0 to m-1
for i=0 to n-1 ! da ((r1-50)*x/100+50),((g1-50)*x/100+50),((b1-50)*x/100+50) a ((r2-50)*x/100+50),((g2-50)*x/100+50),((b2-50)*x/100+50) (riga in basso) e da ((r3-50)*x/100+50),((g3-50)*x/100+50),((b3-50)*x/100+50) a a r4,g4,b4 (riga in alto)
Re=((r1-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1)+(((r2-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r2-50)*x/100+50))/(n-1)-((r1-50)*x/100+50)-j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1))/(m-1)*i
Gr=((g1-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1)+(((g2-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g2-50)*x/100+50))/(n-1)-((g1-50)*x/100+50)-j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1))/(m-1)*i
Bu=((b1-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1)+(((b2-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b2-50)*x/100+50))/(n-1)-((b1-50)*x/100+50)-j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1))/(m-1)*i
DEFINE MATERIAL "cij" w,
Re/100,Gr/100,Bu/100
MATERIAL "cij"
base
vert x/100*cos(j*90/m)*cos(i*120/n),x/100*cos(j*90/m)*sin(i*120/n),x/100*sin(j*90/m)!1
vert x/100*cos(j*90/m)*cos((i+1)*120/n),x/100*cos(j*90/m)*sin((i+1)*120/n),x/100*sin(j*90/m)!2
vert x/100*cos((j+1)*90/m)*cos((i+1)*120/n),x/100*cos((j+1)*90/m)*sin((i+1)*120/n),x/100*sin((j+1)*90/m)!3
vert x/100*cos((j+1)*90/m)*cos(i*120/n),x/100*cos((j+1)*90/m)*sin(i*120/n),x/100*sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
mulz -1
!calotta inferiore lomgitudine 0-120 da green a blue, polo black
r1=not(t)*100
g1=t*100
b1=not(t)*100
r2=not(t)*100
g2=not(t)*100
b2=t*100
r3=0
g3=0
b3=0
for j=0 to m-1
for i=0 to n-1 ! da ((r1-50)*x/100+50),((g1-50)*x/100+50),((b1-50)*x/100+50) a ((r2-50)*x/100+50),((g2-50)*x/100+50),((b2-50)*x/100+50) (riga in basso) e da ((r3-50)*x/100+50),((g3-50)*x/100+50),((b3-50)*x/100+50) a a r4,g4,b4 (riga in alto)
Re=((r1-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1)+(((r2-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r2-50)*x/100+50))/(n-1)-((r1-50)*x/100+50)-j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1))/(m-1)*i
Gr=((g1-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1)+(((g2-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g2-50)*x/100+50))/(n-1)-((g1-50)*x/100+50)-j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1))/(m-1)*i
Bu=((b1-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1)+(((b2-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b2-50)*x/100+50))/(n-1)-((b1-50)*x/100+50)-j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1))/(m-1)*i
DEFINE MATERIAL "dij" w,
Re/100,Gr/100,Bu/100
MATERIAL "dij"
base
vert x/100*cos(j*90/m)*cos(i*120/n),x/100*cos(j*90/m)*sin(i*120/n),x/100*sin(j*90/m)!1
vert x/100*cos(j*90/m)*cos((i+1)*120/n),x/100*cos(j*90/m)*sin((i+1)*120/n),x/100*sin(j*90/m)!2
vert x/100*cos((j+1)*90/m)*cos((i+1)*120/n),x/100*cos((j+1)*90/m)*sin((i+1)*120/n),x/100*sin((j+1)*90/m)!3
vert x/100*cos((j+1)*90/m)*cos(i*120/n),x/100*cos((j+1)*90/m)*sin(i*120/n),x/100*sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
!calotta inferiore lomgitudine 120-240 da blue a red, polo black
r1=not(t)*100
g1=not(t)*100
b1=t*100
r2=t*100
g2=not(t)*100
b2=not(t)*100
r3=0
b3=0
g3=0
for j=0 to m-1
for i=0 to n-1 ! da ((r1-50)*x/100+50),((g1-50)*x/100+50),((b1-50)*x/100+50) a ((r2-50)*x/100+50),((g2-50)*x/100+50),((b2-50)*x/100+50) (riga in basso) e da ((r3-50)*x/100+50),((g3-50)*x/100+50),((b3-50)*x/100+50) a a r4,g4,b4 (riga in alto)
Re=((r1-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1)+(((r2-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r2-50)*x/100+50))/(n-1)-((r1-50)*x/100+50)-j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1))/(m-1)*i
Gr=((g1-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1)+(((g2-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g2-50)*x/100+50))/(n-1)-((g1-50)*x/100+50)-j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1))/(m-1)*i
Bu=((b1-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1)+(((b2-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b2-50)*x/100+50))/(n-1)-((b1-50)*x/100+50)-j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1))/(m-1)*i
DEFINE MATERIAL "eij" w,
Re/100,Gr/100,Bu/100
MATERIAL "eij"
base
vert x/100*cos(j*90/m)*cos(i*120/n),x/100*cos(j*90/m)*sin(i*120/n),x/100*sin(j*90/m)!1
vert x/100*cos(j*90/m)*cos((i+1)*120/n),x/100*cos(j*90/m)*sin((i+1)*120/n),x/100*sin(j*90/m)!2
vert x/100*cos((j+1)*90/m)*cos((i+1)*120/n),x/100*cos((j+1)*90/m)*sin((i+1)*120/n),x/100*sin((j+1)*90/m)!3
vert x/100*cos((j+1)*90/m)*cos(i*120/n),x/100*cos((j+1)*90/m)*sin(i*120/n),x/100*sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
rotz 120
!calotta inferiore lomgitudine 240-360 da red a green, polo black
r1=t*100
g1=not(t)*100
b1=not(t)*100
r2=not(t)*100
g2=t*100
b2=not(t)*100
r3=0
b3=0
g3=0
for j=0 to m-1
for i=0 to n-1 ! da ((r1-50)*x/100+50),((g1-50)*x/100+50),((b1-50)*x/100+50) a ((r2-50)*x/100+50),((g2-50)*x/100+50),((b2-50)*x/100+50) (riga in basso) e da ((r3-50)*x/100+50),((g3-50)*x/100+50),((b3-50)*x/100+50) a a r4,g4,b4 (riga in alto)
Re=((r1-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1)+(((r2-50)*x/100+50)+j*(((r3-50)*x/100+50)-((r2-50)*x/100+50))/(n-1)-((r1-50)*x/100+50)-j*(((r3-50)*x/100+50)-((r1-50)*x/100+50))/(n-1))/(m-1)*i
Gr=((g1-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1)+(((g2-50)*x/100+50)+j*(((g3-50)*x/100+50)-((g2-50)*x/100+50))/(n-1)-((g1-50)*x/100+50)-j*(((g3-50)*x/100+50)-((g1-50)*x/100+50))/(n-1))/(m-1)*i
Bu=((b1-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1)+(((b2-50)*x/100+50)+j*(((b3-50)*x/100+50)-((b2-50)*x/100+50))/(n-1)-((b1-50)*x/100+50)-j*(((b3-50)*x/100+50)-((b1-50)*x/100+50))/(n-1))/(m-1)*i
DEFINE MATERIAL "fij" w,
Re/100,Gr/100,Bu/100
MATERIAL "fij"
base
vert x/100*cos(j*90/m)*cos(i*120/n),x/100*cos(j*90/m)*sin(i*120/n),x/100*sin(j*90/m)!1
vert x/100*cos(j*90/m)*cos((i+1)*120/n),x/100*cos(j*90/m)*sin((i+1)*120/n),x/100*sin(j*90/m)!2
vert x/100*cos((j+1)*90/m)*cos((i+1)*120/n),x/100*cos((j+1)*90/m)*sin((i+1)*120/n),x/100*sin((j+1)*90/m)!3
vert x/100*cos((j+1)*90/m)*cos(i*120/n),x/100*cos((j+1)*90/m)*sin(i*120/n),x/100*sin((j+1)*90/m)!4
edge 1,2,-1,-1,0
edge 2,3,-1,-1,0
edge 3,4,-1,-1,0
edge 4,1,-1,-1,0
pgon 4,0,-1,1,2,3,4
next i
next j
del 6, ntr()-5
return

Anonymous
Not applicable
Options
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
2012-09-19 05:52 PM
2012-09-19
05:52 PM
La costruzione di oggetti GDL fa largo uso degli spostamenti. Infatti un oggetto GDL è formato di più parti che vengono assemblate e ciascuna parte deve essere posizionata in modo appropriato.
La matrice di trasformazione XFORM applica agli oggetti 3D una trasformazione lineare dello spazio. Le trasformazioni lineari comprendono sia le affinità (cioè trasformazioni che cambiano gli angoli e le unità di misura, contraendo o allungando lungo certe direzioni, dove viene comunque mantenuto il parallelismo), che gli spostamenti: traslazioni o rotazioni.
Il vantaggio di utilizzare anche per gli spostamenti la matrice XFORM permette di compiere in un unico passaggio combinazioni di rotazioni e traslazioni che richiederebbero diversi comandi ROT e ADD.
Dato che il calcolatore, nel posizionare gli oggetti, ogni volta si riferisce all’ultima posizione del sistema di assi, che è stato trascinato assieme all’oggetto, rototraslazioni complesse diventano un rompicapo se si usano i comandi ROT e ADD.
La matrice XFORM ha la forma:
XFORM a11, a21, a31, a41
a12, a22, a32, a42
a13, a23, a33, a43
L’ultima colonna:
(a41, a42, a43)
e’ il vettore spostamento che fornisce la nuova origine degli assi.
La prima colonna
(a11, a21, a31)
definisce il nuovo asse x, pertanto se è un versore, cioè sqr(a11^2+ a21^2+ a31^2)=1,
allora non variano le dimensioni lungo le rette parallele all’asse x.
Se invece sqr(a11^2+ a21^2+ a31^2)=L, se L>1 si avrà allungamento lungo l’asse x, per cui lungo tale asse la misura originaria m diventerà m*L.
Analogamente la seconda e terza colonna definiscono rispettivamente i nuovi assi y,z.
Pertanto applicare la matrice XFORM significa effettuare questa operazione:
xx= a11*x+a21*y+a31*z+a41
yy= a12*x+a22*y+a32*z+a42
zz= a13*x+a23*y+a33*z+a43
dove xx,yy,zz sono le nuove coordinate del punto che aveva coordinate x,y,z.
Infatti, ad esempio, il punto (1,0,0) che definiva il versore dell’asse x originario diventa:
(a11+a41, a12+a42, a13+a43)= (a41, a42, a43)+(a11, a12, a13)
Cioè il vettore spostamento dell’origine più il nuovo vettore in cui è stato trasformato il versore di riferimento dell’asse x originario.
Gli oggetti GDL, anche se costituiti da una unica primitiva, se esportati in autocad e richiamati come oggetti GDL si spezzano in diverse combinazioni delle triangolazioni:
PLANE 3, x1,y1,z1, x2,y2,z2, x3,y3, z3
Pertanto come esempio utilizziamo tale PLANE.
Devono essere definiti i valori aij e x1,y1,z1, x2,y2,z2,x3,y3,z3
1) Formula algebrica
xx1= a11*x1+a21*y1+a31*z1+a41
yy1= a12*x1+a22*y1+a32*z1+a42
zz1= a13*x1+a23*y1+a33*z1+a43
xx2= a11*x2+a21*y2+a31*z2+a41
yy2= a12*x2+a22*y2+a32*z2+a42
zz2= a13*x2+a23*y2+a33*z2+a43
xx3= a11*x3+a21*y3+a31*z3+a41
yy3= a12*x3+a22*y3+a32*z3+a42
zz3= a13*x3+a23*y3+a33*z3+a43
PLANE 3, xx1,yy1,zz1, xx2,yy2,zz2, xx3,yy3, zz3
2) Formula con XFORM
XFORM a11, a21, a31, a41
a12, a22, a32, a42
a13, a23, a33, a43
PLANE 3, x1, y1,z1, x2,y2,z2, x3,y3, z3
Le formule 1) e 2) dovrebbero fornire lo stesso risultato.
Tuttavia, anche se più lunga da scrivere, la formula 1) è molto più generale, permette infatti di applicare non solo trasformazioni lineari, ma qualsiasi tipo di trasformazione:
xx1= f1(x1,y1,z1)
yy1= f2(x1,y1,z1)
zz1= f3(x1,y1,z1)
xx2= f1(x2,y2,z2)
yy2= f2(x2,y2,z2)
zz2= f3(x2,y2,z2)
xx3= f1(x3,y3,z3)
yy3= f2(x3,y3,z3)
zz3= f3(x3,y3,z3)
PLANE 3, xx1,yy1,zz1, xx2,yy2,zz2, xx3,yy3,zz3
Dove f1,f2,f3 sono funzioni a tre variabili.
!end. EXAMPLE:
!!!Istruzioni per ottenere l'oggetto GDL in figura
!Elenco parametri -------------------------------------------:
x=1
y=1
z=0.2
f=45 !rotazione antioraria attorno ad asse verticale
t=30 !rotazione antioraria attorno ad asse orizzontale
r=25 !rollio attorno all'asse normale rispetto top di block
x0=1 !traslazioni
y0=.4
x0=.3
p=21 !pen
o=1 !bit mostra project2
c=238 !index material
! TESTO 2D --------------------------------------------------:
poly2 4,7, x0,y0, !0,0,0
(cos(f)*cos(t)*cos(r)-sin(f)*sin(r))*x+x0,
(sin(f)*cos(t)*cos(r)+cos(f)*sin(r))*x+y0, ! x,0,0
(cos(f)*cos(t)*cos(r)-sin(f)*sin(r))*x-(cos(f)*cos(t)*sin(r)+sin(f)*cos(r))*y +x0,
(sin(f)*cos(t)*cos(r)+cos(f)*sin(r))*x+(-sin(f)*cos(t)*sin(r)+cos(f)*cos(r))*y+y0, ! x,y,0
-(cos(f)*cos(t)*sin(r)+sin(f)*cos(r))*y+x0,
(-sin(f)*cos(t)*sin(r)+cos(f)*cos(r))*y+y0! 0,y,0
poly2 4,7, cos(f)*sin(t)*z+x0,sin(f)*sin(t)*z+y0, !0,0,z
(cos(f)*cos(t)*cos(r)-sin(f)*sin(r))*x+cos(f)*sin(t)*z+x0,
(sin(f)*cos(t)*cos(r)+cos(f)*sin(r))*x+sin(f)*sin(t)*z+y0, ! x,0,z
(cos(f)*cos(t)*cos(r)-sin(f)*sin(r))*x-(cos(f)*cos(t)*sin(r)+sin(f)*cos(r))*y +cos(f)*sin(t)*z+x0,
(sin(f)*cos(t)*cos(r)+cos(f)*sin(r))*x+(-sin(f)*cos(t)*sin(r)+cos(f)*cos(r))*y+sin(f)*sin(t)*z+y0, ! x,y,z
-(cos(f)*cos(t)*sin(r)+sin(f)*cos(r))*y +cos(f)*sin(t)*z+x0,
(-sin(f)*cos(t)*sin(r)+cos(f)*cos(r))*y+sin(f)*sin(t)*z+y0 ! 0,y,z
line2 x0,y0,cos(f)*sin(t)*z+x0,sin(f)*sin(t)*z+y0 !collegamento 0,0,0 - 0,0,z
line2 (cos(f)*cos(t)*cos(r)-sin(f)*sin(r))*x+x0,(sin(f)*cos(t)*cos(r)+cos(f)*sin(r))*x+y0,
(cos(f)*cos(t)*cos(r)-sin(f)*sin(r))*x+cos(f)*sin(t)*z+x0,(sin(f)*cos(t)*cos(r)+cos(f)*sin(r))*x+sin(f)*sin(t)*z+y0 !collegamento x,0,0 - x,0,z
line2 (cos(f)*cos(t)*cos(r)-sin(f)*sin(r))*x-(cos(f)*cos(t)*sin(r)+sin(f)*cos(r))*y +x0,
(sin(f)*cos(t)*cos(r)+cos(f)*sin(r))*x+(-sin(f)*cos(t)*sin(r)+cos(f)*cos(r))*y+y0,
(cos(f)*cos(t)*cos(r)-sin(f)*sin(r))*x-(cos(f)*cos(t)*sin(r)+sin(f)*cos(r))*y +cos(f)*sin(t)*z+x0,
(sin(f)*cos(t)*cos(r)+cos(f)*sin(r))*x+(-sin(f)*cos(t)*sin(r)+cos(f)*cos(r))*y+sin(f)*sin(t)*z+y0 !collegamento x,y,0 - x,y,z
line2 -(cos(f)*cos(t)*sin(r)+sin(f)*cos(r))*y+x0,(-sin(f)*cos(t)*sin(r)+cos(f)*cos(r))*y+y0,
-(cos(f)*cos(t)*sin(r)+sin(f)*cos(r))*y +cos(f)*sin(t)*z+x0,(-sin(f)*cos(t)*sin(r)+cos(f)*cos(r))*y+sin(f)*sin(t)*z+y0 !collegamento 0,y,0 - 0,y,z
pen p
if o=1 then project2 3,270,2
!TESTO 3D----------------------------------------------------:
pen p
material c
XFORM cos(f)*cos(t)*cos(r)-sin(f)*sin(r),-cos(f)*cos(t)*sin(r)-sin(f)*cos(r), cos(f)*sin(t), x0,
sin(f)*cos(t)*cos(r)+cos(f)*sin(r),-sin(f)*cos(t)*sin(r)+cos(f)*cos(r), sin(f)*sin(t), y0,
-sin(t)*cos(r) , sin(t)*sin(r), cos(t), z0
block x,y,z
!Commento ---------------------------------------------------:
La verifica con project 2 mostra la correttezza della formula 2D
Angolo t rappresenta azimut (angolo rispetto asse x equivalente singolarmente a rot z)
Angolo f rappresenta latitudine (angolo rispetto piano xy equivalente singolarmente a rot f, f positivo la figura scende)
Angolo r rappresenta rollio (angolo di rotazione attorno alla normale del piano di base, xy equivalente singolarmente a rot z,
tuttavia quando la figura ha ruotato di t e z, l'angolo del rollio farà girare la figura attorno all'asse che in origine era z).
XFORM x1,x2,x3,x0,
y1,y2,y3,y0,
z1,z2,z3,z0
applicato al punto (x,y,z)
lo sposta nel punto (x1*x+x2*y+x3*z+x0,y1*x+y2*y+y3*z+y0,z1*x+z2*y+z3*z+z0)
infatti gli assi coordinati con versori (1,0,0),(0,1,0),(0,0,1),
vedono trasformati tali versori rispettivamente in:
(x1*1+x2*0+x3*0+x0,y1*1+y2*0+y3*0+y0,z1*1+z2*0+z3*0+z0)=(x1+x0,y1+y0,z1+z0)=(x1,y1,z1)+(x0,y0,z0)
(x2+x0,y2+y0,z2+z0)=(x2,y2,z2)+(x0,y0,z0)
(x3+x0,y3+y0,z3+z0)=(x3,y3,z3)+(x0,y0,z0)
dove i primi vettori, colonne di XFORM, indicano rotazioni ed allungamenti degli assi,
mentre (x0,y0,z0) è la traslazione dell' origine.
Pertanto la trasformazione:
XFORM cos(f)*cos(t)*cos(r)-sin(f)*sin(r),-cos(f)*cos(t)*sin(r)-sin(f)*cos(r), cos(f)*sin(t), 0,
sin(f)*cos(t)*cos(r)+cos(f)*sin(r),-sin(f)*cos(t)*sin(r)+cos(f)*cos(r), sin(f)*sin(t), 0,
-sin(t)*cos(r) , sin(t)*sin(r), cos(t), 0
che può essere riscritta:
x1=cos(f)*cos(t)*cos(r)-sin(f)*sin(r)
y1=sin(f)*cos(t)*cos(r)+cos(f)*sin(r)
z1=-sin(t)*cos(r)
x2=-cos(f)*cos(t)*sin(r)-sin(f)*cos(r)
y2=-sin(f)*cos(t)*sin(r)+cos(f)*cos(r)
z2=sin(t)*sin(r)
x3=cos(f)*sin(t)
y3=sin(f)*sin(t)
z3=cos(t)
XFORM x1,x2,x3,0,
y1,y2,y3,0,
z1,z2,z3,0
applicata al punto (x,y,z) lo trasforma in (x_,y_,z_)
x_=x1*x+x2*y+x3*z
y_=y1*x+y2*y+y3*z
z_=z1*x+z2*y+z3*z
cioè in forma estesa:
x= !ascissa vertice
y= !ordinata vertice
z= !quota vertice
x_=(cos(f)*cos(t)*cos(r)-sin(f)*sin(r))*x+(-cos(f)*cos(t)*sin(r)-sin(f)*cos(r))*y+cos(f)*sin(t)*z
y_=(sin(f)*cos(t)*cos(r)+cos(f)*sin(r))*x+(-sin(f)*cos(t)*sin(r)+cos(f)*cos(r))*y+sin(f)*sin(t)*z
z_=sin(-t)*cos(r)*x+sin(t)*sin(r)*y+cos(t)*z
dove (x_,y_) rappresenta la sua nuova proiezione ortogonale su xy.
La matrice di trasformazione XFORM applica agli oggetti 3D una trasformazione lineare dello spazio. Le trasformazioni lineari comprendono sia le affinità (cioè trasformazioni che cambiano gli angoli e le unità di misura, contraendo o allungando lungo certe direzioni, dove viene comunque mantenuto il parallelismo), che gli spostamenti: traslazioni o rotazioni.
Il vantaggio di utilizzare anche per gli spostamenti la matrice XFORM permette di compiere in un unico passaggio combinazioni di rotazioni e traslazioni che richiederebbero diversi comandi ROT e ADD.
Dato che il calcolatore, nel posizionare gli oggetti, ogni volta si riferisce all’ultima posizione del sistema di assi, che è stato trascinato assieme all’oggetto, rototraslazioni complesse diventano un rompicapo se si usano i comandi ROT e ADD.
La matrice XFORM ha la forma:
XFORM a11, a21, a31, a41
a12, a22, a32, a42
a13, a23, a33, a43
L’ultima colonna:
(a41, a42, a43)
e’ il vettore spostamento che fornisce la nuova origine degli assi.
La prima colonna
(a11, a21, a31)
definisce il nuovo asse x, pertanto se è un versore, cioè sqr(a11^2+ a21^2+ a31^2)=1,
allora non variano le dimensioni lungo le rette parallele all’asse x.
Se invece sqr(a11^2+ a21^2+ a31^2)=L, se L>1 si avrà allungamento lungo l’asse x, per cui lungo tale asse la misura originaria m diventerà m*L.
Analogamente la seconda e terza colonna definiscono rispettivamente i nuovi assi y,z.
Pertanto applicare la matrice XFORM significa effettuare questa operazione:
xx= a11*x+a21*y+a31*z+a41
yy= a12*x+a22*y+a32*z+a42
zz= a13*x+a23*y+a33*z+a43
dove xx,yy,zz sono le nuove coordinate del punto che aveva coordinate x,y,z.
Infatti, ad esempio, il punto (1,0,0) che definiva il versore dell’asse x originario diventa:
(a11+a41, a12+a42, a13+a43)= (a41, a42, a43)+(a11, a12, a13)
Cioè il vettore spostamento dell’origine più il nuovo vettore in cui è stato trasformato il versore di riferimento dell’asse x originario.
Gli oggetti GDL, anche se costituiti da una unica primitiva, se esportati in autocad e richiamati come oggetti GDL si spezzano in diverse combinazioni delle triangolazioni:
PLANE 3, x1,y1,z1, x2,y2,z2, x3,y3, z3
Pertanto come esempio utilizziamo tale PLANE.
Devono essere definiti i valori aij e x1,y1,z1, x2,y2,z2,x3,y3,z3
1) Formula algebrica
xx1= a11*x1+a21*y1+a31*z1+a41
yy1= a12*x1+a22*y1+a32*z1+a42
zz1= a13*x1+a23*y1+a33*z1+a43
xx2= a11*x2+a21*y2+a31*z2+a41
yy2= a12*x2+a22*y2+a32*z2+a42
zz2= a13*x2+a23*y2+a33*z2+a43
xx3= a11*x3+a21*y3+a31*z3+a41
yy3= a12*x3+a22*y3+a32*z3+a42
zz3= a13*x3+a23*y3+a33*z3+a43
PLANE 3, xx1,yy1,zz1, xx2,yy2,zz2, xx3,yy3, zz3
2) Formula con XFORM
XFORM a11, a21, a31, a41
a12, a22, a32, a42
a13, a23, a33, a43
PLANE 3, x1, y1,z1, x2,y2,z2, x3,y3, z3
Le formule 1) e 2) dovrebbero fornire lo stesso risultato.
Tuttavia, anche se più lunga da scrivere, la formula 1) è molto più generale, permette infatti di applicare non solo trasformazioni lineari, ma qualsiasi tipo di trasformazione:
xx1= f1(x1,y1,z1)
yy1= f2(x1,y1,z1)
zz1= f3(x1,y1,z1)
xx2= f1(x2,y2,z2)
yy2= f2(x2,y2,z2)
zz2= f3(x2,y2,z2)
xx3= f1(x3,y3,z3)
yy3= f2(x3,y3,z3)
zz3= f3(x3,y3,z3)
PLANE 3, xx1,yy1,zz1, xx2,yy2,zz2, xx3,yy3,zz3
Dove f1,f2,f3 sono funzioni a tre variabili.
!end. EXAMPLE:
!!!Istruzioni per ottenere l'oggetto GDL in figura
!Elenco parametri -------------------------------------------:
x=1
y=1
z=0.2
f=45 !rotazione antioraria attorno ad asse verticale
t=30 !rotazione antioraria attorno ad asse orizzontale
r=25 !rollio attorno all'asse normale rispetto top di block
x0=1 !traslazioni
y0=.4
x0=.3
p=21 !pen
o=1 !bit mostra project2
c=238 !index material
! TESTO 2D --------------------------------------------------:
poly2 4,7, x0,y0, !0,0,0
(cos(f)*cos(t)*cos(r)-sin(f)*sin(r))*x+x0,
(sin(f)*cos(t)*cos(r)+cos(f)*sin(r))*x+y0, ! x,0,0
(cos(f)*cos(t)*cos(r)-sin(f)*sin(r))*x-(cos(f)*cos(t)*sin(r)+sin(f)*cos(r))*y +x0,
(sin(f)*cos(t)*cos(r)+cos(f)*sin(r))*x+(-sin(f)*cos(t)*sin(r)+cos(f)*cos(r))*y+y0, ! x,y,0
-(cos(f)*cos(t)*sin(r)+sin(f)*cos(r))*y+x0,
(-sin(f)*cos(t)*sin(r)+cos(f)*cos(r))*y+y0! 0,y,0
poly2 4,7, cos(f)*sin(t)*z+x0,sin(f)*sin(t)*z+y0, !0,0,z
(cos(f)*cos(t)*cos(r)-sin(f)*sin(r))*x+cos(f)*sin(t)*z+x0,
(sin(f)*cos(t)*cos(r)+cos(f)*sin(r))*x+sin(f)*sin(t)*z+y0, ! x,0,z
(cos(f)*cos(t)*cos(r)-sin(f)*sin(r))*x-(cos(f)*cos(t)*sin(r)+sin(f)*cos(r))*y +cos(f)*sin(t)*z+x0,
(sin(f)*cos(t)*cos(r)+cos(f)*sin(r))*x+(-sin(f)*cos(t)*sin(r)+cos(f)*cos(r))*y+sin(f)*sin(t)*z+y0, ! x,y,z
-(cos(f)*cos(t)*sin(r)+sin(f)*cos(r))*y +cos(f)*sin(t)*z+x0,
(-sin(f)*cos(t)*sin(r)+cos(f)*cos(r))*y+sin(f)*sin(t)*z+y0 ! 0,y,z
line2 x0,y0,cos(f)*sin(t)*z+x0,sin(f)*sin(t)*z+y0 !collegamento 0,0,0 - 0,0,z
line2 (cos(f)*cos(t)*cos(r)-sin(f)*sin(r))*x+x0,(sin(f)*cos(t)*cos(r)+cos(f)*sin(r))*x+y0,
(cos(f)*cos(t)*cos(r)-sin(f)*sin(r))*x+cos(f)*sin(t)*z+x0,(sin(f)*cos(t)*cos(r)+cos(f)*sin(r))*x+sin(f)*sin(t)*z+y0 !collegamento x,0,0 - x,0,z
line2 (cos(f)*cos(t)*cos(r)-sin(f)*sin(r))*x-(cos(f)*cos(t)*sin(r)+sin(f)*cos(r))*y +x0,
(sin(f)*cos(t)*cos(r)+cos(f)*sin(r))*x+(-sin(f)*cos(t)*sin(r)+cos(f)*cos(r))*y+y0,
(cos(f)*cos(t)*cos(r)-sin(f)*sin(r))*x-(cos(f)*cos(t)*sin(r)+sin(f)*cos(r))*y +cos(f)*sin(t)*z+x0,
(sin(f)*cos(t)*cos(r)+cos(f)*sin(r))*x+(-sin(f)*cos(t)*sin(r)+cos(f)*cos(r))*y+sin(f)*sin(t)*z+y0 !collegamento x,y,0 - x,y,z
line2 -(cos(f)*cos(t)*sin(r)+sin(f)*cos(r))*y+x0,(-sin(f)*cos(t)*sin(r)+cos(f)*cos(r))*y+y0,
-(cos(f)*cos(t)*sin(r)+sin(f)*cos(r))*y +cos(f)*sin(t)*z+x0,(-sin(f)*cos(t)*sin(r)+cos(f)*cos(r))*y+sin(f)*sin(t)*z+y0 !collegamento 0,y,0 - 0,y,z
pen p
if o=1 then project2 3,270,2
!TESTO 3D----------------------------------------------------:
pen p
material c
XFORM cos(f)*cos(t)*cos(r)-sin(f)*sin(r),-cos(f)*cos(t)*sin(r)-sin(f)*cos(r), cos(f)*sin(t), x0,
sin(f)*cos(t)*cos(r)+cos(f)*sin(r),-sin(f)*cos(t)*sin(r)+cos(f)*cos(r), sin(f)*sin(t), y0,
-sin(t)*cos(r) , sin(t)*sin(r), cos(t), z0
block x,y,z
!Commento ---------------------------------------------------:
La verifica con project 2 mostra la correttezza della formula 2D
Angolo t rappresenta azimut (angolo rispetto asse x equivalente singolarmente a rot z)
Angolo f rappresenta latitudine (angolo rispetto piano xy equivalente singolarmente a rot f, f positivo la figura scende)
Angolo r rappresenta rollio (angolo di rotazione attorno alla normale del piano di base, xy equivalente singolarmente a rot z,
tuttavia quando la figura ha ruotato di t e z, l'angolo del rollio farà girare la figura attorno all'asse che in origine era z).
XFORM x1,x2,x3,x0,
y1,y2,y3,y0,
z1,z2,z3,z0
applicato al punto (x,y,z)
lo sposta nel punto (x1*x+x2*y+x3*z+x0,y1*x+y2*y+y3*z+y0,z1*x+z2*y+z3*z+z0)
infatti gli assi coordinati con versori (1,0,0),(0,1,0),(0,0,1),
vedono trasformati tali versori rispettivamente in:
(x1*1+x2*0+x3*0+x0,y1*1+y2*0+y3*0+y0,z1*1+z2*0+z3*0+z0)=(x1+x0,y1+y0,z1+z0)=(x1,y1,z1)+(x0,y0,z0)
(x2+x0,y2+y0,z2+z0)=(x2,y2,z2)+(x0,y0,z0)
(x3+x0,y3+y0,z3+z0)=(x3,y3,z3)+(x0,y0,z0)
dove i primi vettori, colonne di XFORM, indicano rotazioni ed allungamenti degli assi,
mentre (x0,y0,z0) è la traslazione dell' origine.
Pertanto la trasformazione:
XFORM cos(f)*cos(t)*cos(r)-sin(f)*sin(r),-cos(f)*cos(t)*sin(r)-sin(f)*cos(r), cos(f)*sin(t), 0,
sin(f)*cos(t)*cos(r)+cos(f)*sin(r),-sin(f)*cos(t)*sin(r)+cos(f)*cos(r), sin(f)*sin(t), 0,
-sin(t)*cos(r) , sin(t)*sin(r), cos(t), 0
che può essere riscritta:
x1=cos(f)*cos(t)*cos(r)-sin(f)*sin(r)
y1=sin(f)*cos(t)*cos(r)+cos(f)*sin(r)
z1=-sin(t)*cos(r)
x2=-cos(f)*cos(t)*sin(r)-sin(f)*cos(r)
y2=-sin(f)*cos(t)*sin(r)+cos(f)*cos(r)
z2=sin(t)*sin(r)
x3=cos(f)*sin(t)
y3=sin(f)*sin(t)
z3=cos(t)
XFORM x1,x2,x3,0,
y1,y2,y3,0,
z1,z2,z3,0
applicata al punto (x,y,z) lo trasforma in (x_,y_,z_)
x_=x1*x+x2*y+x3*z
y_=y1*x+y2*y+y3*z
z_=z1*x+z2*y+z3*z
cioè in forma estesa:
x= !ascissa vertice
y= !ordinata vertice
z= !quota vertice
x_=(cos(f)*cos(t)*cos(r)-sin(f)*sin(r))*x+(-cos(f)*cos(t)*sin(r)-sin(f)*cos(r))*y+cos(f)*sin(t)*z
y_=(sin(f)*cos(t)*cos(r)+cos(f)*sin(r))*x+(-sin(f)*cos(t)*sin(r)+cos(f)*cos(r))*y+sin(f)*sin(t)*z
z_=sin(-t)*cos(r)*x+sin(t)*sin(r)*y+cos(t)*z
dove (x_,y_) rappresenta la sua nuova proiezione ortogonale su xy.
Anonymous
Not applicable
Options
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
2012-09-19 10:13 PM
2012-09-19
10:13 PM
Il linguaggio GDL prevede rotazioni e traslazioni. La difficoltà nell’effettuare i movimenti è che ogni volta viene trascinato il sistema di riferimento assieme all’oggetto in una nuova posizione, così che il nuovo movimento viene calcolato a partire da quest’ultima. Per le sole traslazioni non ci sono problemi, ma quando si effettuano rotazioni, queste cambiano anche i valori delle traslazioni; inoltre ogni rotazione viene sempre effettuata attorno all’origine degli assi, riferita all’ultima posizione L, non a quella globale iniziale G.
Per chiarire con un esercizio come funzionano le cose considero il solo movimento su piano.
Premetto alcuni concetti che sono di aiuto per semplificare le cose.
Nella teoria dei vettori bidimensionali esiste un particolare ambito che è quello dei numeri complessi:
un numero complesso è un vettore (x,y) espresso nella forma: x+i*y, dove i rappresenta la parte detta immaginaria, che altro non è che il versore dell’asse y=(0,1). Il prodotto si esegue normalmente come per i numeri reali, con la sola differenza che i^2=-1, fatto che non rappresenta un assurdo. Infatti in questo caso il prodotto esprime una rotazione attorno all’origine.
Un vettore (x,y) può sempre essere scritto nella forma: sqr(x^2+x^2)*(cos(al), sin(al)),
dove sqr(x^2+x^2) è il modulo o lunghezza del vettore, al è l’angolo che il vettore forma con l’asse x.
Valgono le formule: al=acs(x/sqr(x^2+x^2)) oppure al=asn(y/sqr(x^2+x^2)) o ancora, per -90<al<90, al=atn(y/x). Infatti:
x= sqr(x^2+x^2)*cos(al), y= sqr(x^2+x^2)*sin(al), y=x*tan(al)
Il prodotto fra due vettori espressi come numeri complessi, fornisce un terzo vettore, dove il modulo risulta essere il prodotto tra i moduli, mentre l’angolo al è dato dalla somma dei due angoli originari.
Ricordare questa proprietà permette di ricavare, senza bisogno di manuali, diverse formule di trigonometria ed in particolare la formula per ruotare un vettore dato attorno all’origine.
Come esempio ruotiamo il punto (x,y) di un angolo be (ricordando che i^2=-1) :
(x+i*y)*(cos(be)+i*sin(be)) = x*cos(be)-y*sin(be) +i*( y*cos(be)+x*sin(be) )
Il numero complesso ottenuto è il vettore ( x*cos(be)-y*sin(be), x*sin(be)+y*cos(be) )
Pertanto queste sono pure le nuove coordinate del vettore (x,y) ruotato dell’angolo al, formula che corrisponde nel linguaggio GDL a:
rot2 be
Esempio:
rot2 be
line2 x1,y1, x2,y2
del 1 !cancella l’ultimo movimento
equivale a:
xa= x1*cos(be)-y1*sin(be)
ya= x1*sin(be)+y1*cos(be)
xb= x2*cos(be)-y2*sin(be)
yb= x2*sin(be)+y2*cos(be)
line2 xa,ya, xb,yb
Vogliamo ora ricavare una formula per spostare un oggetto da un punto A1=(xa1,ya1) a un punto A2=(xa2,ya2), facendolo poi ruotare di un angolo be.
nel linguaggio GDL:
add2 xa2-xa1, ya2-ya1
rot2 be
line2 x1,y1, x2,y2
del 2 !cancella gli ultimi 2 movimenti
L’oggetto ruoterà attorno a quel punto che inizialmente costituiva l’origine e che attualmente ha coordinate assolute xa2-xa1, ya2-ya1. L’ordine dei movimenti non può essere scambiato.
Altrimenti occorrerebbe scrivere:
rot2 be
(xa2-xa1)*cos(-be)- (ya2-ya1)*sin(-be) , (xa2-xa1)*cos(-be)+(ya2-ya1)*sin(-be)
Questo perché, avendo effettuato la rotazione, il vettore spostamento viene ora visto ruotato di –be.
Le trasformazioni di coordinate equivalgono a:
xa= x1*cos(be) - y1*sin(be) + xa2-xa1
ya= x1*sin(be) +y1*cos(be) + ya2-ya1
xb= x2*cos(be)- y2*sin(be) + xa2-xa1
yb= x2*sin(be) +y2*cos(be)+ ya2-ya1
line2 xa,ya, xb,yb
Più complesso è far ruotare un oggetto di un angolo be non attorno all’origine, ma attorno a un determinate punto C di cooordinate xc,yc. In questo caso occorre considerare un nuovo oggetto identico, ma spostato del vettore (-xc,-yc)
Le trasformazioni di coordinate equivalgono a:
xa= (x1-xc)*cos(be) - (y1-yc)*sin(be) +xc
ya= (x1-xc)*sin(be) +(y1-yc)*cos(be) +yc
xb= (x2-xc)*cos(be) - (y2-yc)*sin(be) +xc
yb= (x2-xc)*sin(be) +(y2-yc)*cos(be) +yc
line2 xa,ya, xb,yb
L’origine attorno a cui avviene la rotazione sarà, relativamente all’oggetto, il punto C, che però ora coincide con l’origine, effettuata poi la rotazione occorre traslare il tutto secondo il vettore OC, ma poiché è avvenuta la rotazione, il vettore spostamento non è più (xc,yc) , ma:
xc*cos(-be)- yc*sin(-be) , yc*cos(-be)+xc*sin(-be)
Pertanto nel linguaggio GDL:
rot2 be
add2 –xc +xc*cos(be)+ yc*sin(be) , -yc+ yc*cos(be)-xc*sin(be)
line2 x1,y1, x2,y2
del 2
Se poi si volesse traslare il tutto di x,y:
add2 x,y
rot2 be
add2 –xc +xc*cos(be)+ yc*sin(be) , -yc+ yc*cos(be)-xc*sin(be)
line2 x1,y1, x2,y2
del 3
I movimenti rigidi del piano, anche se composti di rotazione e traslazione, possono essere ridotti ad una unica rotazione, considerando una eventuale traslazione come una rotazione con centro all’infinito.
Per verificare la validità delle formule con un oggetto GDL non troppo elementare, vogliamo determinare il centro di rotazione di un versore che si sposta dalla posizione A1 alla posizione A2, ruotando di be.
Le coordinate del versore iniziale sono (cos(ga),sin(ga)) con punto di applicazione A1=(xa1,ya1),
le coordinate del versore finale sono (cos(ga+be),sin(ga+be)) con punto di applicazione A2=(xa2,ya2).
Il centro di rotazione C si trova sull’asse del segmento A1-A2, il cui punto medio M ha coordinate:
xm=(xa1+xa2)/2
ym=(ya1+ya2)/2
Costruendo il triangolo isoscele A1-A2-C è evidente che l’angolo A1-C-A2 ha ampiezza be, se infatti per ipotesi il versore iniziale fosse ortogonale a C-A1, cioè tangente al cerchio con centro C per A1, il versore finale sarebbe ancora tangente al cerchio, essendo poi ruotato di be, l’angolo al centro deve valere appunto be. Posto d=A1-A2, risulta:
d=sqr((xa2-xa1)^2+(ya2-ya1)^2)
detta h l’altezza del triangolo A1-A2-C, risulta: d/2=h*tan(be/2)
h=d/(2* tan(be/2))
Il raggio del cerchio, cioè il lato del triangolo C-A1:
r=sqr(d^2/4+h^2)
L’inclinazione del vettore A1-A2 è data dall’angolo al:
al=acs( (xa2-xa1)/d )
Poiché il centro C si trova sull’asse di A1-A2 a distanza h, le sue coordinate sono:
xc=xm-h*sin(al)
yc=ym+h*cos(al)
Di fatto abbiamo determinato il centro xc,yc dell’arco A1-A2, dato l’angolo al centro be:
xa1=
ya1=
xa2=
ya2=
be= !fine parametri
xm=(xa1+xa2)/2
ym=(ya1+ya2)/2
d=sqr((xa2-xa1)^2+(ya2-ya1)^2)
h=d/(2* tan(be/2))
al=acs( (xa2-xa1)/d )
r=sqr(d^2/4+h^2) !raggio
xc=xm-h*sin(al)
yc=ym+h*cos(al)
!!!Istruzioni per ottenere l'oggetto GDL in figura:
!Elenco parametri -------------------------------------------:
xa1=0 !coord. A1
ya1=0
xa2=2 !coord. A2
ya2=.6
ga=25
be=45
v="vettore definito" !abc
!Script parametri -------------------------------------------:
values "v" "vettore definito","ruotato con GDL","ruotato con trasformazione"
! TESTO 2D --------------------------------------------------:
xm=(xa1+xa2)/2
ym=(ya1+ya2)/2
d=sqr((xa2-xa1)^2+(ya2-ya1)^2)
al=acs( (xa2-xa1)/d )
h=d/(2* tan(be/2))
r=sqr(d^2/4+h^2) !raggio
xc=xm-h*sin(al)
yc=ym+h*cos(al)
pen 21
line2 xa1,ya1, xa2,ya2
line2 xc,yc, xm,ym
line2 xc,yc, xa2,ya2
line2 xa1,ya1, xc,yc
arc2 xc,yc,r,-90+al-be/2,-90+al+be/2
pen 20
line2 xa1,ya1,xa1+cos(ga),ya1+sin(ga)
line2 xa2,ya2,xa2+cos(ga),ya2+sin(ga)
if v="vettore definito" goto 1
if v="ruotato con GDL" goto 2
if v="ruotato con trasformazione" goto 3
1:line2 xa2,ya2,xa2+cos(ga+be),ya2+sin(ga+be)
end
2:pen 6
rot2 be
add2 -xc +xc*cos(be)+ yc*sin(be) , -yc+ yc*cos(be)-xc*sin(be)
line2 xa1,ya1,xa1+cos(ga),ya1+sin(ga)
del 2
end
3:pen 4
xa= (xa1-xc)*cos(be) - (ya1-yc)*sin(be) +xc
ya= (xa1-xc)*sin(be) +(ya1-yc)*cos(be) +yc
xb= (xa1+cos(ga)-xc)*cos(be) -(ya1+sin(ga)-yc)*sin(be) +xc
yb= (xa1+cos(ga)-xc)*sin(be) +(ya1+sin(ga)-yc)*cos(be) +yc
line2 xa,ya, xb,yb
!Commento ------------------------------------:
Il vettore con punto di applicazione A1 e direzione definita dall'angolo ga rispetto x,
dopo una rototraslazione si trova con punto di applicazione in A2 e risulta ruotato di be.
Il nuovo angolo del vettore su x è ga+be.
Si richiede di trovare quel punto C sul piano tale che,
tramite rotazione attorno a C,
sposta il vettore dato dalla posizione 1 alla posizione 2.
Per chiarire con un esercizio come funzionano le cose considero il solo movimento su piano.
Premetto alcuni concetti che sono di aiuto per semplificare le cose.
Nella teoria dei vettori bidimensionali esiste un particolare ambito che è quello dei numeri complessi:
un numero complesso è un vettore (x,y) espresso nella forma: x+i*y, dove i rappresenta la parte detta immaginaria, che altro non è che il versore dell’asse y=(0,1). Il prodotto si esegue normalmente come per i numeri reali, con la sola differenza che i^2=-1, fatto che non rappresenta un assurdo. Infatti in questo caso il prodotto esprime una rotazione attorno all’origine.
Un vettore (x,y) può sempre essere scritto nella forma: sqr(x^2+x^2)*(cos(al), sin(al)),
dove sqr(x^2+x^2) è il modulo o lunghezza del vettore, al è l’angolo che il vettore forma con l’asse x.
Valgono le formule: al=acs(x/sqr(x^2+x^2)) oppure al=asn(y/sqr(x^2+x^2)) o ancora, per -90<al<90, al=atn(y/x). Infatti:
x= sqr(x^2+x^2)*cos(al), y= sqr(x^2+x^2)*sin(al), y=x*tan(al)
Il prodotto fra due vettori espressi come numeri complessi, fornisce un terzo vettore, dove il modulo risulta essere il prodotto tra i moduli, mentre l’angolo al è dato dalla somma dei due angoli originari.
Ricordare questa proprietà permette di ricavare, senza bisogno di manuali, diverse formule di trigonometria ed in particolare la formula per ruotare un vettore dato attorno all’origine.
Come esempio ruotiamo il punto (x,y) di un angolo be (ricordando che i^2=-1) :
(x+i*y)*(cos(be)+i*sin(be)) = x*cos(be)-y*sin(be) +i*( y*cos(be)+x*sin(be) )
Il numero complesso ottenuto è il vettore ( x*cos(be)-y*sin(be), x*sin(be)+y*cos(be) )
Pertanto queste sono pure le nuove coordinate del vettore (x,y) ruotato dell’angolo al, formula che corrisponde nel linguaggio GDL a:
rot2 be
Esempio:
rot2 be
line2 x1,y1, x2,y2
del 1 !cancella l’ultimo movimento
equivale a:
xa= x1*cos(be)-y1*sin(be)
ya= x1*sin(be)+y1*cos(be)
xb= x2*cos(be)-y2*sin(be)
yb= x2*sin(be)+y2*cos(be)
line2 xa,ya, xb,yb
Vogliamo ora ricavare una formula per spostare un oggetto da un punto A1=(xa1,ya1) a un punto A2=(xa2,ya2), facendolo poi ruotare di un angolo be.
nel linguaggio GDL:
add2 xa2-xa1, ya2-ya1
rot2 be
line2 x1,y1, x2,y2
del 2 !cancella gli ultimi 2 movimenti
L’oggetto ruoterà attorno a quel punto che inizialmente costituiva l’origine e che attualmente ha coordinate assolute xa2-xa1, ya2-ya1. L’ordine dei movimenti non può essere scambiato.
Altrimenti occorrerebbe scrivere:
rot2 be
(xa2-xa1)*cos(-be)- (ya2-ya1)*sin(-be) , (xa2-xa1)*cos(-be)+(ya2-ya1)*sin(-be)
Questo perché, avendo effettuato la rotazione, il vettore spostamento viene ora visto ruotato di –be.
Le trasformazioni di coordinate equivalgono a:
xa= x1*cos(be) - y1*sin(be) + xa2-xa1
ya= x1*sin(be) +y1*cos(be) + ya2-ya1
xb= x2*cos(be)- y2*sin(be) + xa2-xa1
yb= x2*sin(be) +y2*cos(be)+ ya2-ya1
line2 xa,ya, xb,yb
Più complesso è far ruotare un oggetto di un angolo be non attorno all’origine, ma attorno a un determinate punto C di cooordinate xc,yc. In questo caso occorre considerare un nuovo oggetto identico, ma spostato del vettore (-xc,-yc)
Le trasformazioni di coordinate equivalgono a:
xa= (x1-xc)*cos(be) - (y1-yc)*sin(be) +xc
ya= (x1-xc)*sin(be) +(y1-yc)*cos(be) +yc
xb= (x2-xc)*cos(be) - (y2-yc)*sin(be) +xc
yb= (x2-xc)*sin(be) +(y2-yc)*cos(be) +yc
line2 xa,ya, xb,yb
L’origine attorno a cui avviene la rotazione sarà, relativamente all’oggetto, il punto C, che però ora coincide con l’origine, effettuata poi la rotazione occorre traslare il tutto secondo il vettore OC, ma poiché è avvenuta la rotazione, il vettore spostamento non è più (xc,yc) , ma:
xc*cos(-be)- yc*sin(-be) , yc*cos(-be)+xc*sin(-be)
Pertanto nel linguaggio GDL:
rot2 be
add2 –xc +xc*cos(be)+ yc*sin(be) , -yc+ yc*cos(be)-xc*sin(be)
line2 x1,y1, x2,y2
del 2
Se poi si volesse traslare il tutto di x,y:
add2 x,y
rot2 be
add2 –xc +xc*cos(be)+ yc*sin(be) , -yc+ yc*cos(be)-xc*sin(be)
line2 x1,y1, x2,y2
del 3
I movimenti rigidi del piano, anche se composti di rotazione e traslazione, possono essere ridotti ad una unica rotazione, considerando una eventuale traslazione come una rotazione con centro all’infinito.
Per verificare la validità delle formule con un oggetto GDL non troppo elementare, vogliamo determinare il centro di rotazione di un versore che si sposta dalla posizione A1 alla posizione A2, ruotando di be.
Le coordinate del versore iniziale sono (cos(ga),sin(ga)) con punto di applicazione A1=(xa1,ya1),
le coordinate del versore finale sono (cos(ga+be),sin(ga+be)) con punto di applicazione A2=(xa2,ya2).
Il centro di rotazione C si trova sull’asse del segmento A1-A2, il cui punto medio M ha coordinate:
xm=(xa1+xa2)/2
ym=(ya1+ya2)/2
Costruendo il triangolo isoscele A1-A2-C è evidente che l’angolo A1-C-A2 ha ampiezza be, se infatti per ipotesi il versore iniziale fosse ortogonale a C-A1, cioè tangente al cerchio con centro C per A1, il versore finale sarebbe ancora tangente al cerchio, essendo poi ruotato di be, l’angolo al centro deve valere appunto be. Posto d=A1-A2, risulta:
d=sqr((xa2-xa1)^2+(ya2-ya1)^2)
detta h l’altezza del triangolo A1-A2-C, risulta: d/2=h*tan(be/2)
h=d/(2* tan(be/2))
Il raggio del cerchio, cioè il lato del triangolo C-A1:
r=sqr(d^2/4+h^2)
L’inclinazione del vettore A1-A2 è data dall’angolo al:
al=acs( (xa2-xa1)/d )
Poiché il centro C si trova sull’asse di A1-A2 a distanza h, le sue coordinate sono:
xc=xm-h*sin(al)
yc=ym+h*cos(al)
Di fatto abbiamo determinato il centro xc,yc dell’arco A1-A2, dato l’angolo al centro be:
xa1=
ya1=
xa2=
ya2=
be= !fine parametri
xm=(xa1+xa2)/2
ym=(ya1+ya2)/2
d=sqr((xa2-xa1)^2+(ya2-ya1)^2)
h=d/(2* tan(be/2))
al=acs( (xa2-xa1)/d )
r=sqr(d^2/4+h^2) !raggio
xc=xm-h*sin(al)
yc=ym+h*cos(al)
!!!Istruzioni per ottenere l'oggetto GDL in figura:
!Elenco parametri -------------------------------------------:
xa1=0 !coord. A1
ya1=0
xa2=2 !coord. A2
ya2=.6
ga=25
be=45
v="vettore definito" !abc
!Script parametri -------------------------------------------:
values "v" "vettore definito","ruotato con GDL","ruotato con trasformazione"
! TESTO 2D --------------------------------------------------:
xm=(xa1+xa2)/2
ym=(ya1+ya2)/2
d=sqr((xa2-xa1)^2+(ya2-ya1)^2)
al=acs( (xa2-xa1)/d )
h=d/(2* tan(be/2))
r=sqr(d^2/4+h^2) !raggio
xc=xm-h*sin(al)
yc=ym+h*cos(al)
pen 21
line2 xa1,ya1, xa2,ya2
line2 xc,yc, xm,ym
line2 xc,yc, xa2,ya2
line2 xa1,ya1, xc,yc
arc2 xc,yc,r,-90+al-be/2,-90+al+be/2
pen 20
line2 xa1,ya1,xa1+cos(ga),ya1+sin(ga)
line2 xa2,ya2,xa2+cos(ga),ya2+sin(ga)
if v="vettore definito" goto 1
if v="ruotato con GDL" goto 2
if v="ruotato con trasformazione" goto 3
1:line2 xa2,ya2,xa2+cos(ga+be),ya2+sin(ga+be)
end
2:pen 6
rot2 be
add2 -xc +xc*cos(be)+ yc*sin(be) , -yc+ yc*cos(be)-xc*sin(be)
line2 xa1,ya1,xa1+cos(ga),ya1+sin(ga)
del 2
end
3:pen 4
xa= (xa1-xc)*cos(be) - (ya1-yc)*sin(be) +xc
ya= (xa1-xc)*sin(be) +(ya1-yc)*cos(be) +yc
xb= (xa1+cos(ga)-xc)*cos(be) -(ya1+sin(ga)-yc)*sin(be) +xc
yb= (xa1+cos(ga)-xc)*sin(be) +(ya1+sin(ga)-yc)*cos(be) +yc
line2 xa,ya, xb,yb
!Commento ------------------------------------:
Il vettore con punto di applicazione A1 e direzione definita dall'angolo ga rispetto x,
dopo una rototraslazione si trova con punto di applicazione in A2 e risulta ruotato di be.
Il nuovo angolo del vettore su x è ga+be.
Si richiede di trovare quel punto C sul piano tale che,
tramite rotazione attorno a C,
sposta il vettore dato dalla posizione 1 alla posizione 2.
Anonymous
Not applicable
Options
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
2014-04-02 04:01 PM
2014-04-02
04:01 PM
I'm italian, if Goggle translate fails i can try to explain the text.
If asked i can even translate the posts.
Let me know.
If asked i can even translate the posts.
Let me know.
Suggested content
- DWG import/export in Collaboration with other software
- Backup Script for BIMcloud Basic 2025 in Teamwork & BIMcloud
- Correct the Italian translation of the material "aluminum" from "aLuminio" to "aLLuminio" in Project data & BIM
- PLEASE fix your website Italian translation in General discussions
- Sending a value from 3D Script to parameter in Libraries & objects
