- Graphisoft Community (INT)
- :
- Forum
- :
- Modeling
- :
- How to create a superellipse.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Pin this post for me
- Bookmark
- Subscribe to Topic
- Mute
- Printer Friendly Page
How to create a superellipse.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
2009-03-25 12:12 PM
I'm looking for a way to draw/generate a 2d superellipse (or something close- as the shape might not be precisely this) in plan- perhaps then after extrude it and round the edges to form the basic shape of a building.

Is this possible?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
2009-03-30 09:00 PM
Erika wrote:I'd guess this one:
...Is it this Superellipse?
Or ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
2009-03-30 09:07 PM
Though it does seem to be a little shifty from pic to pic.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
2009-03-30 10:16 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
2009-03-31 07:05 AM
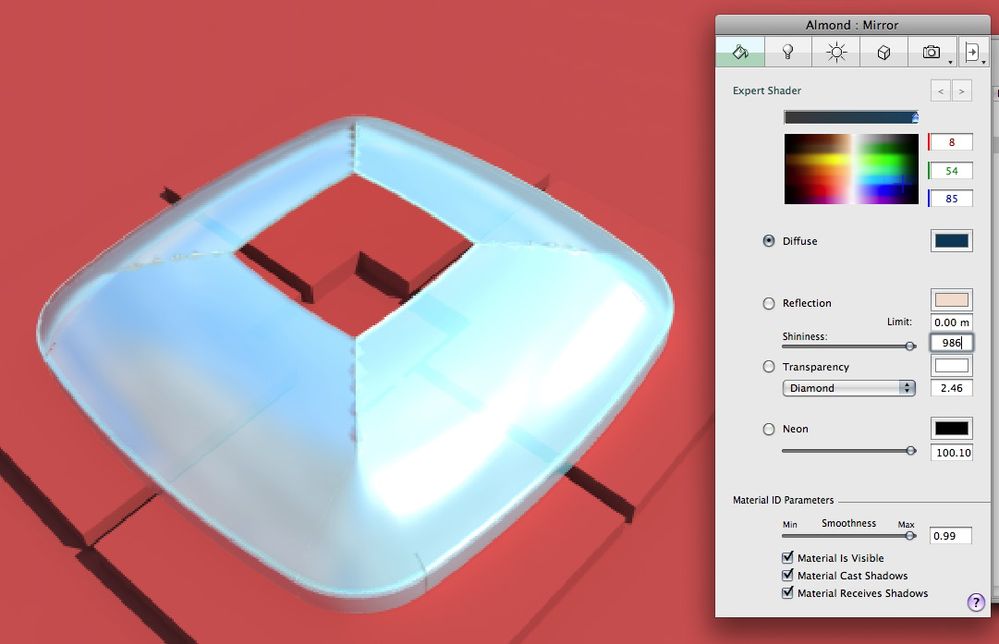
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
2009-03-31 07:47 AM
I should probably also look into some more advanced tutorials- seems like I've only scratched the surface with the one that comes with the program.
Thanks)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
2009-03-31 05:35 PM
After you read this:
complex profile stuff
you are up-to-speed
You really need Experimentorials™ for this.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
2009-04-05 05:38 PM
borki wrote:
Hey all, this is my first post, so I hope it falls in the right place.
I'm looking for a way to draw/generate a 2d superellipse (or something close- as the shape might not be precisely this) in plan- perhaps then after extrude it and round the edges to form the basic shape of a building.
Is this possible?
Did you try this object?
Windows 10 x64
Since ArchiCAD 9
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
2012-11-09 09:10 PM
Make Piet Hein smile.
Any GDL wizards up to the challenge?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
2012-11-14 09:10 PM
A superellipse may be described parametrically byWouldn't this be a cool shape to have in one's palette?
x = a*cos^(2/r)t
y = b*sin^(2/r)t.
The restriction to r>2 is sometimes made.
Superellipses with a=b are also known as Lamé curves or Lamé ovals, and the case a=b with r=4 is sometimes known as the squircle. By analogy, the superellipse with a!=b and r=4 might be termed the rectellipse.
http://mathworld.wolfram.com/Superellipse.html
- « Previous
-
- 1
- 2
- Next »
- « Previous
-
- 1
- 2
- Next »
- Creating a 3D BIMx model in BIMx
- Zone tool gives the dreaded 'no closed polygon... etc' error message in Modeling
- Export plan view as image format (to create 'blueprint' style) in Documentation
- Create MappingDefinitions.json with LP_XMLConverter in Libraries & objects
- MODELING OF WINDOWS USING THE CURTAIN WALL TOOL in Modeling
