MOD operator

[Anonymous]

Here is the result I get when calculating

A=120 cm
B=40 cm

A mod B = 0.4 !!!!

When using PRINT A, I get 1.2, meaning that AC use the values in meter, thus
1.2 mod 0.4 = 0.4

But, in my point of view the rest of the divion is zero !

Is this normal ? I just want a function that will tell me if a multiple of B can fit exactly in A...

My only solution at the present time is to use A*1000 mod B*1000 (so I have a precision of 1 millimeter), but I think this might be a bug...

[Anonymous]

As the multiplication trick isn't correct, I decided to use the definition of the MOD function :
X MOD Y = X - Y * INT (X/Y)

When applied to X=1.2 and Y=0.4, the result is :
-2.22045e-0.16... I know this is very small and wouldn't be a problem on site , but I thought the result should have been 0

[Karl Ottenstein]

Geoffroy wrote:
but I thought the result should have been 0

Hi Geoffroy,

You've run into numerical discretization error that results from computers using binary arithmetic. Decimal fractions cannot be represented precisely in a fixed number of binary digits (bits) - and therefore some truncation occurs. This numerical error is magnified when arithmetic is performed, particularly subtraction which can leave nothing but the error remaining. The branch of Computer Science/Mathematics called 'Numerical Analysis' deals with these issues and more.

There is no problem if you are using MOD with integer (whole) values.

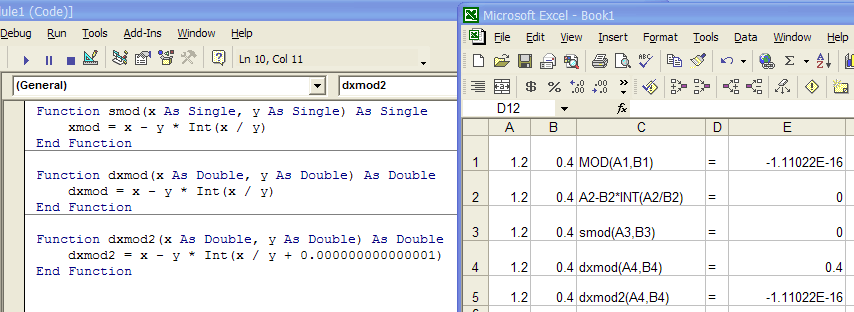
Attached is a screenshot of an Excel spreadsheet and the results of computing the same expression as you used in five different ways.

Row 1 uses the Excel MOD operator - and the result looks strange, as did yours. Decimal fractions generate infinitely repeating binary fractions - and so when a number is stored in a fixed number of bits, part of the number is lost. You're seeing that those missing bits result in an error of:
0.0000000000000001
which is pretty tiny after all .. but is certainly not zero. I talked about this on GDLTalk a while back - and which is probably where this conversation belongs, except that I cannot post screenshots there. One needs to allow for this numerical error with some kind of factor, epsilon, and realize that the result will be within +/- epsilon of the true result. In this case, anything that is between + or - 1E-15 could safely be said to be zero. As you say, for construction purposes, we could set epsilon to be much larger and still call it zero.

Row 2 miraculously shows zero using just your forumula. The following three rows explore this further.

Row 3 uses the function smod defined in VisualBasic in the module at the left and uses single precision arithmetic - which is apparently the default precision of Excel since this row and row 2 both give 0. Now, single precision should exhibit the same kind of numerical error - but at 1E-8 or so, so I think we just had good luck here.

Row 4 shows the next VB function - same formula but with double precision values and arithmetic. Pretty odd, yes? It gives the 0.4 value that you got from ArchiCAD - which suggests to me that the ArchiCAD implementation of the MOD function is incorrect. The reason is easy to see. INT(X/Y) evaluated to 2 instead of 3 - thus giving the result of 0.4. Well, how can this be? Simply because INT truncates (chops) the fraction from a number leaving the whole part. If the result of the division was 2.999999999999999 then the result of the INT would indeed be 2. Why all the 9's? Same deal as above.

Row 5 shows one solution to implementing the MOD function - and the result matches exactly line 1, which is the Excel built-in MOD function. Here, I added an epsilon factor of 1E-15 to the result of the division to balance the numerical error. In some case, I might get 3.000000000000001 or slightly more, but for the MOD function this doesn't matter, since INT will chop it all off.

Whew. Looks like you did find a bug to report to GS, though!

Regards,
Karl

[Oleg]

Geoffroy wrote:
Here is the result I get when calculating

A=120 cm
B=40 cm

A mod B = 0.4 !!!!

If you want to use the MOD:
eps=0.0001 ! tolerance
rmd=A MOD B
IF ABS(rmd)<eps OR ABS(B-rmd)<eps THEN ...

other vatiant:
IF ABS(A-B*INT(A/B+0.5))<eps THEN ...

PS: On A mod B = 0.4 !!!!
Lets for example, 0.4 in a PC processor is 0.40000000001
then 1.2 MOD 0.40000000001=3.999999999
Rounds by PRINT is 0.4

Oleg

[Red]

Geoffroy wrote:
When using PRINT A, I get 1.2, meaning that AC use the values in meter, thus
1.2 mod 0.4 = 0.4

I'm still fairly new to GDL, but many of the people helping me with GDL that have background with other scripting languages always ask about a PRINT so it will show the value. Are you scripting straight through Archicad to do this or is it 3rd party program.